Arkusz egzaminacyjny, Wydawnictwo: CKE

Zadanie 13, a) - strona 24

Wyznacz objętość $\text{[math]}$ graniastosłupa prawidłowego czworokątnego $\text{[math]}$ przedstawionego na rysunku, w zależności od wysokości $\text{[math]}$ w którym odcinek łączący punkt przecięcia przekątnych jednej podstawy z dowolnym wierzchołkiem drugiej podstawy ma długość $\text{[math]}$ oraz podaj dziedzinę funkcji $\text{[math]}$

$\text{[math]}$ - wysokość graniastosłupa

$\text{[math]}$ – krawędź postawy

$\text{[math]}$ – przekątna podstawy

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

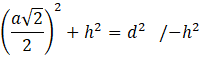
ODP: Objętość graniastosłupa w zależności od wysokości $\text{[math]}$ jest opisana równaniem $\text{[math]}$ , którego dziedziną jest $\text{[math]}$

Oznacz jako:

$\text{[math]}$ - wysokość graniastosłupa

$\text{[math]}$ – krawędź postawy

$\text{[math]}$ – przekątna podstawy

Zauważ, że połowa przekątnej podstawy, krawędź boczna i odcinek długości $\text{[math]}$ tworzą trójkąt prostokątny. Skorzystaj z twierdzenia Pitagorasa, aby wyznaczyć długość boku $\text{[math]}$ w zależności od zmiennych $\text{[math]}$ i $\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

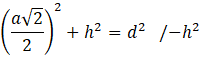
Zauważ, że długość boku musi być dodatnia:

$\text{[math]}$

Wyznacz zbiór rozwiązań dla których wyznaczona wartość $\text{[math]}$ jest dodatnia.

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

Oznacza to, że dziedziną są wszystkie $\text{[math]}$ należące do przedziału $\text{[math]}$ .

Wyznacz objętość graniastosłupa.

$\text{[math]}$

Pod powyższe równanie podstaw wyliczoną wartość $\text{[math]}$ . Zauważ, że powstanie funkcja zmiennej $\text{[math]}$

$\text{[math]}$

Zadanie 30., strona 103, Matematyka z plusem. Klasa 4. Zbiór zadań - rozwiązania i odpowiedzi

Zadanie 1.19., strona 17, Prosto do matury. Klasa 4. Podręcznik. Zakres podstawowy - rozwiązania i odpowiedzi

Ćwiczenie 12., strona 51, Matematyka wokół nas. Klasa 6. Zeszyt ćwiczeń. Część 2 – rozwiązania i odpowiedzi

Zadanie 4., strona 127, MATeMAtyka. Klasa 3. Zbiór zadań. Zakres podstawowy – rozwiązania i odpowiedzi

Zadanie 25, strona 17, Matematyka z kluczem. Klasa 6. Zbiór zadań - rozwiązania i odpowiedzi

Zadanie 14., strona 179, Matematyka. Klasa 7. Zbiór zadań – rozwiązania i odpowiedzi

Zadanie 2., strona 236, Matematyka wokół nas. Klasa 8. Podręcznik - rozwiązania i odpowiedzi

Zadanie Łamigłówka nr 5., strona 42, Matematyka z plusem. Klasa 4. Zbiór zadań - rozwiązania i odpowiedzi

Ćwiczenie „Co było na lekcji?” 3/3, strona 95, Matematyka. Klasa 4. Zeszyt ćwiczeń. Część 1 - rozwiązania i odpowiedzi

Zadanie 16., strona 73, Matematyka z kluczem. Klasa 7. Zbiór zadań - rozwiązania i odpowiedzi

4

5

6

7

8

10

12

14

16

18

20

22

Zadanie 13

24

24

24

Pełny spis treści