![]()
![]()
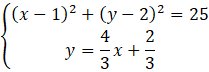
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
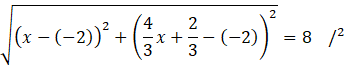
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
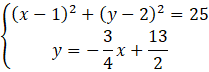
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
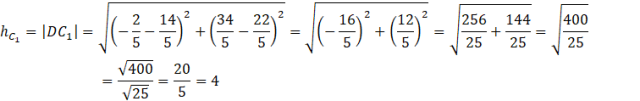
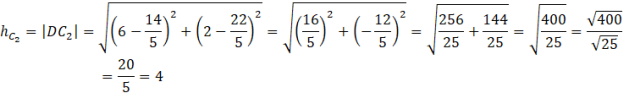
![]()
ODP: Pole trójkąta ABC wynosi 20.

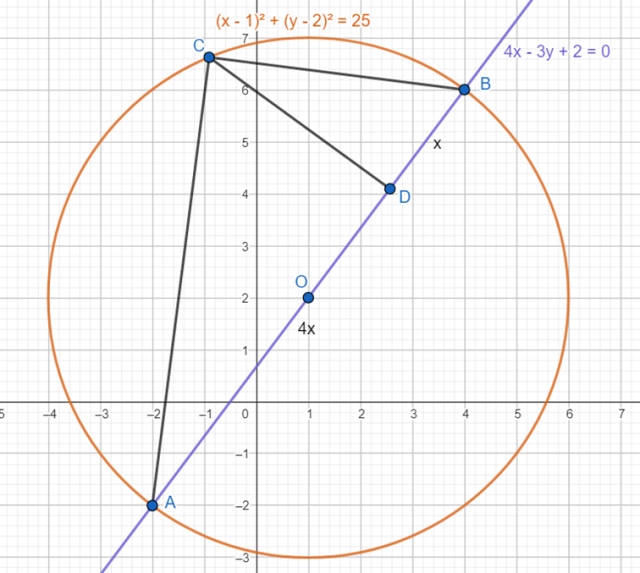
Wykonaj rysunek pomocniczy:
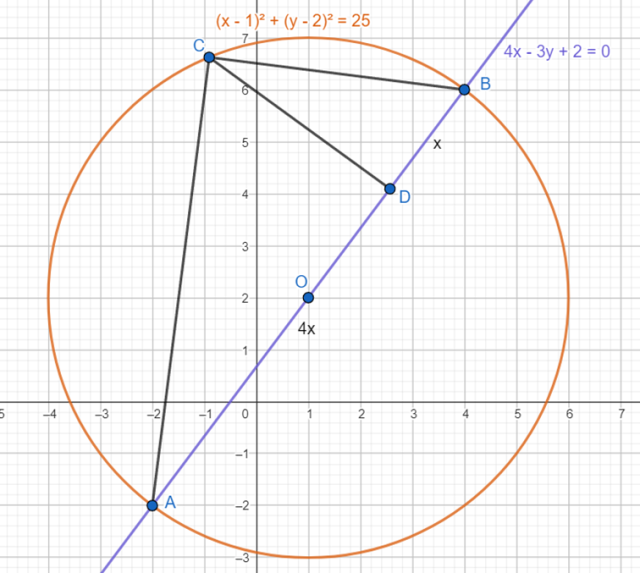
Oblicz współrzędne przecięcia prostej
![]() i okręgu, czyli współrzędne punktów A i B. Zrobisz to rozwiązując układ dwóch równań będącymi wzorami obu tych funkcji.
i okręgu, czyli współrzędne punktów A i B. Zrobisz to rozwiązując układ dwóch równań będącymi wzorami obu tych funkcji.
![]()
Z drugiego równania wyznacz wartość
![]() .
.
![]()
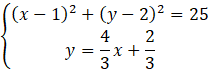
Podstaw wartość
![]() z drugiego równania pod pierwsze.
z drugiego równania pod pierwsze.
![]()
Z powstałego równania wyznacz wartość
![]()
![]()
![]()
![]()
![]()
![]()
Oblicz deltę i miejsca zerowe powstałego równania.
![]()
![]()
![]()
![]()
Zauważ, że znasz pierwsze współrzędne obu punktów, na tej podstawie oblicz ich drugą współrzędną.
![]()
![]()
Zapisz współrzędne punktów A i B.
![]()
Oblicz długość odcinka AB, czyli średnicę okręgu o środku O.
![]()
Skorzystaj z tego, że
![]() i oblicz długości odcinków AD i DB.
i oblicz długości odcinków AD i DB.
![]()
![]()
![]()
Zapisz współrzędne punktu D, skorzystaj z tego, że leży on na prostej AB.
![]()
Skorzystaj ze wzoru na długość odcinka AD. Podstaw znane wartości i wyznacz z niego wartość
![]()
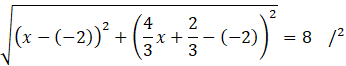
![]()
Skorzystaj ze wzoru skróconego mnożenia na kwadrat sumy:
![]()
![]()
![]()
Oblicz deltę i miejsca zerowe powstałego równania.
![]()
![]()
![]()
![]()
![]()
![]()
Zauważ, że punkt
![]() musi mieć współrzędne:
musi mieć współrzędne:
![]() ponieważ dla punktu
ponieważ dla punktu
![]() nie leżałby na okręgu.
nie leżałby na okręgu.
Zapisz wzór na równanie kierunkowe prostej przechodzącej przez punkty C i D.
![]()
Zauważ, że prosta CD zawiera wysokość trójkąta ABC opadającą na bok AB, więc jest prostopadła do prostej
![]()
![]()
Współczynnik kierunkowy prostych prostopadłych jest przeciwny i odwrotny, na tej podstawie oblicz współczynnik kierunkowy szukanej prostej.
![]()
![]()
![]()
Skorzystaj z tego, że prosta CD przechodzi przez punkt D. Wstaw jego współrzędne w miejsce
![]() i
i
![]() i oblicz wartość współczynnika
i oblicz wartość współczynnika
![]()
![]()
![]()
![]()
Zapisz równanie szukanej prostej CD.
![]()
Oblicz współrzędne przecięcia prostej CD i okręgu, czyli współrzędne punktu C. Zrobisz to rozwiązując układ dwóch równań będącymi wzorami obu tych funkcji.
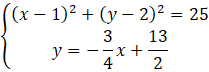
Podstaw wartość
![]() z drugiego równania pod pierwsze.
z drugiego równania pod pierwsze.
![]()
Z powstałego równania oblicz wartość
![]()
![]()
Skorzystaj ze wzoru skróconego mnożenia na kwadrat różnicy:
![]()
![]()
![]()
![]()
Oblicz deltę i miejsca zerowe powstałego równania.
![]()
![]()
![]()
![]()
![]()
![]()
Zapisz współrzędne punktu C.
![]()
Oblicz długość odcinków
![]() i
i
![]() , czyli wysokości trójkąta ABC.
, czyli wysokości trójkąta ABC.
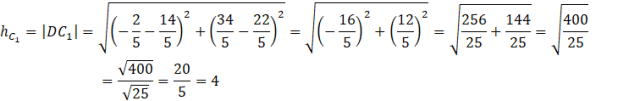
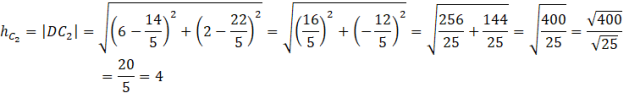
Zauważ, że w obu przypadkach wysokość trójkąta jest taka sama. Możesz więc obliczyć pole trójkąta ABC.
![]()