W tym zadaniu musisz wykazać, że równanie
![]() będzie miało nieskończenie wiele rozwiązań wtedy i tylko wtedy, gdy odległość między liczbami a i b jest równa 1.
będzie miało nieskończenie wiele rozwiązań wtedy i tylko wtedy, gdy odległość między liczbami a i b jest równa 1.
Załóżmy, że:
![]()
Gdy
![]() to wyrażenie
to wyrażenie
![]() będzie równe 0 oraz gdy
będzie równe 0 oraz gdy
![]() to wyrażenie
to wyrażenie
![]() będzie równe 0, więc korzystając z definicji wartości bezwzględnej, zapisujemy:
będzie równe 0, więc korzystając z definicji wartości bezwzględnej, zapisujemy:
![]()
![]()
Informację te przedstawmy na rysunku pomocniczym:
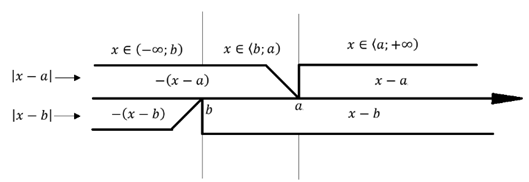
Rozważamy trzy przypadki, w których zapisujemy równanie bez symbolu wartości bezwzględnej:
1.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Istnieje jedno rozwiązanie.
2.
![]()
![]()
![]()
![]()
Gdy
![]() to rozwiązaniem równania
to rozwiązaniem równania
![]() jest dowolna liczba, lecz musi ona spełniać postawiony warunek, dlatego przyjmujemy, że rozwiązaniem równania
jest dowolna liczba, lecz musi ona spełniać postawiony warunek, dlatego przyjmujemy, że rozwiązaniem równania
![]() są liczby z przedziału
są liczby z przedziału
![]() . W przedziale
. W przedziale
![]() między liczbami b i a zawiera się nieskończenie wiele liczb, więc gdy odległość między liczbami a i b wyrażona w sposób
między liczbami b i a zawiera się nieskończenie wiele liczb, więc gdy odległość między liczbami a i b wyrażona w sposób
![]() będzie równa 1, to równanie
będzie równa 1, to równanie
![]() będzie miało nieskończenie wiele rozwiązań.
będzie miało nieskończenie wiele rozwiązań.
3.
![]()
![]()
![]()
![]()
![]()
Istnieje jedno rozwiązanie.

Pamiętaj, że liczby a i b traktujemy jako stałe niewiadome, a nie jako zmienne. Gdy założymy, że
![]() to otrzymamy te same wyniki, tylko warunki z podpunktów się zmienią. Odległość liczb a i b równą 1 zapisujemy w sposób
to otrzymamy te same wyniki, tylko warunki z podpunktów się zmienią. Odległość liczb a i b równą 1 zapisujemy w sposób
![]() . Założyliśmy, że
. Założyliśmy, że
![]() , dlatego
, dlatego
![]() , dzięki czemu możemy wykazać, że gdy
, dzięki czemu możemy wykazać, że gdy
![]() to otrzymujemy tożsamość z drugiego podpunktu.
to otrzymujemy tożsamość z drugiego podpunktu.

Ćwiczenie A.
92Przykład 1.
92Przykład 2.
93Przykład 3.
93Zadanie 1.
94Zadanie 2.
94Zadanie 3.
94Zadanie 4.
94Zadanie 5.
94Zadanie 6.
94Zadanie 2.
98Zadanie 16.
100Zadanie 17.
101Ćwiczenie A.
102Ćwiczenie B.
103Przykład 1.
103Zadanie 2.
104Zadanie 3.
104Zadanie 4.
104Zadanie 5.
104Zadanie 6.
105Zadanie 8.
105Zadanie 10.
105Zadanie 15.
106Przykład 1.
108Przykład 2.
108Przykład 3.
109Zadanie 1.
110Zadanie 3.
110Zadanie 4.
110Zadanie 5.
110Zadanie 6.
110Zadanie 7.
110Zadanie 9.
110Zadanie 10.
111Ćwiczenie B.
112Zadanie 1.
116Zadanie 2.
116Zadanie 3.
116Zadanie 4.
116Zadanie 7.
116Ćwiczenie A.
117Przykład 2.
119Przykład 3.
119Przykład 4.
120Przykład 5.
120Zadanie 3.
121Zadanie 4.
121Zadanie 5.
121Zadanie 6.
121Zadanie 7.
121Zadanie 8.
122Zadanie 9.
122Zadanie 10.
122Zadanie 11.
122Zadanie 13.
122Zadanie 14.
122Zadanie 16.
123Zadanie 20.
124Zadanie 21.
124Zadanie 23.
124Przykład 1.
126Przykład C.
127Zadanie 3.
127Zadanie 5.
128Zadanie 6.
128Zadanie 1.
130Zadanie 4.
130Zadanie 17.
132Zadanie 1.
134Zadanie 2.
134Zadanie 3.
134Zadanie 4.
134Zadanie 5.
134Zadanie 7.
134Zadanie 8.
134
