W tym zadaniu musisz rozwiązać równanie
![]() i zaznaczyć odpowiedź, która zawiera sumę rozwiązań tego równania.
i zaznaczyć odpowiedź, która zawiera sumę rozwiązań tego równania.
![]()
![]()
1.
![]()
![]()
![]()
![]()
![]()
![]() , więc nie jest rozwiązaniem tego równania.
, więc nie jest rozwiązaniem tego równania.
2.
![]()
![]()
![]()
![]()
![]()
![]()
![]() , więc jest rozwiązaniem tego równania.
, więc jest rozwiązaniem tego równania.
3.
![]()
![]()
![]()
![]()
![]()
![]()
![]() , więc jest rozwiązaniem tego równania.
, więc jest rozwiązaniem tego równania.
Równanie
![]() ma dwa rozwiązania
ma dwa rozwiązania
![]() i
i
![]() .
.
![]()
Odp. C.
![]()

Rozwiązujemy równanie
![]() .
.
Najpierw sprawdzamy, kiedy wyrażenia
![]() i
i
![]() będą równe 0:
będą równe 0:
![]()
![]()
![]()
![]()
![]()
Gdy
![]() to wyrażenie
to wyrażenie
![]() będzie równe 0 oraz gdy
będzie równe 0 oraz gdy
![]() to wyrażenie
to wyrażenie
![]() będzie równe 0, więc korzystając z definicji wartości bezwzględnej, zapisujemy:
będzie równe 0, więc korzystając z definicji wartości bezwzględnej, zapisujemy:
![]()
![]()
Informację te przedstawmy na rysunku pomocniczym:
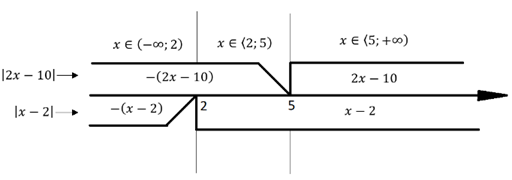
Rozważamy trzy przypadki, w których zapisujemy równanie bez symbolu wartości bezwzględnej. Rozwiązujemy je i sprawdzamy, czy otrzymana liczba zawiera w przedziale:
1.
![]()
![]()
![]()
![]()
![]()
![]() , więc nie jest rozwiązaniem tego równania.
, więc nie jest rozwiązaniem tego równania.
2.
![]()
![]()
![]()
![]()
![]()
![]()
![]() , więc jest rozwiązaniem tego równania.
, więc jest rozwiązaniem tego równania.
3.
![]()
![]()
![]()
![]()
![]()
![]()
![]() , więc jest rozwiązaniem tego równania.
, więc jest rozwiązaniem tego równania.
Z powyższych obliczeń wynika, że równanie
![]() ma dwa rozwiązania
ma dwa rozwiązania
![]() i
i
![]() . Obliczmy sumę tych rozwiązań:
. Obliczmy sumę tych rozwiązań:
![]()
Odp. C.
![]() jest prawidłowa.
jest prawidłowa.

Ćwiczenie A.
92Przykład 1.
92Przykład 2.
93Przykład 3.
93Zadanie 1.
94Zadanie 2.
94Zadanie 3.
94Zadanie 4.
94Zadanie 5.
94Zadanie 6.
94Zadanie 2.
98Zadanie 16.
100Zadanie 17.
101Ćwiczenie A.
102Ćwiczenie B.
103Przykład 1.
103Zadanie 2.
104Zadanie 3.
104Zadanie 4.
104Zadanie 5.
104Zadanie 6.
105Zadanie 8.
105Zadanie 10.
105Zadanie 15.
106Przykład 1.
108Przykład 2.
108Przykład 3.
109Zadanie 1.
110Zadanie 3.
110Zadanie 4.
110Zadanie 5.
110Zadanie 6.
110Zadanie 7.
110Zadanie 9.
110Zadanie 10.
111Ćwiczenie B.
112Zadanie 1.
116Zadanie 2.
116Zadanie 3.
116Zadanie 4.
116Zadanie 7.
116Ćwiczenie A.
117Przykład 2.
119Przykład 3.
119Przykład 4.
120Przykład 5.
120Zadanie 3.
121Zadanie 4.
121Zadanie 5.
121Zadanie 6.
121Zadanie 7.
121Zadanie 8.
122Zadanie 9.
122Zadanie 10.
122Zadanie 11.
122Zadanie 13.
122Zadanie 14.
122Zadanie 16.
123Zadanie 20.
124Zadanie 21.
124Zadanie 23.
124Przykład 1.
126Przykład C.
127Zadanie 3.
127Zadanie 5.
128Zadanie 6.
128Zadanie 1.
130Zadanie 4.
130Zadanie 17.
132Zadanie 1.
134Zadanie 2.
134Zadanie 3.
134Zadanie 4.
134Zadanie 5.
134Zadanie 7.
134Zadanie 8.
134
