W tym zadaniu musisz zaznaczyć odpowiedź, która posiada nierówność, która ma w swoim rozwiązaniu najwięcej liczb całkowitych.
Rozwiążmy nierówność
![]() :
:
![]() i
i
![]()
![]() i
i
![]()
![]() i
i
![]()
![]()
W tym przedziale znajduje się 5 liczb całkowitych.
Rozwiążmy nierówność
![]() :
:
![]() i
i
![]()
![]() i
i
![]()
![]() i
i
![]()
![]()
W tym przedziale znajduje się 17 liczb całkowitych.
Rozwiążmy nierówność
![]() :
:
![]() i
i
![]()
![]() i
i
![]()
![]() i
i
![]()
![]()
W tym przedziale znajduje się 2 liczby całkowite.
Rozwiążmy nierówność
![]() :
:
![]() i
i
![]()
![]() i
i
![]()
![]() i
i
![]()
![]()
W tym przedziale znajduje się 1 liczba całkowita.
Odp. B
![]()

Rozwiąż wszystkie nierówności i sprawdź, która z nich ma najwięcej liczb całkowitych w swoim rozwiązaniu. Zacznijmy od nierówności
![]() . Wyrażenie w wartości bezwzględnej musi być mniejsze bądź równe 4 i większe bądź równe –4, zatem:
. Wyrażenie w wartości bezwzględnej musi być mniejsze bądź równe 4 i większe bądź równe –4, zatem:
![]() i
i
![]()
![]() i
i
![]()
![]() i
i
![]()
Zaznaczamy na osi liczbowej zbiory rozwiązań nierówności i ich część wspólną, która jest rozwiązaniem nierówności
![]() :
:

Więc:
![]()
W tym przedziale znajduje się 5 liczb całkowitych. Pamiętaj, że zaliczamy też –5 i –1, ponieważ przedział jest obustronnie domknięty.
Rozwiążmy nierówność
![]() . Wyrażenie w wartości bezwzględnej musi być mniejsze od 3 i większe od –3, zatem:
. Wyrażenie w wartości bezwzględnej musi być mniejsze od 3 i większe od –3, zatem:
![]() i
i
![]()
![]() i
i
![]()
![]() i
i
![]()
Zaznaczamy na osi liczbowej zbiory rozwiązań nierówności i ich część wspólną, która jest rozwiązaniem nierówności
![]() :
:

Więc:
![]()
W tym przedziale znajduje się 17 liczb całkowitych. Pamiętaj, że nie liczymy –27 i –9, ponieważ przedział jest obustronnie otwarty.
Rozwiążmy nierówność
![]() . Wyrażenie w wartości bezwzględnej musi być mniejsze bądź równe 2 i większe bądź równe –2, zatem:
. Wyrażenie w wartości bezwzględnej musi być mniejsze bądź równe 2 i większe bądź równe –2, zatem:
![]() i
i
![]()
![]() i
i
![]()
![]() i
i
![]()
Zaznaczamy na osi liczbowej zbiory rozwiązań nierówności i ich część wspólną, która jest rozwiązaniem nierówności
![]() :
:
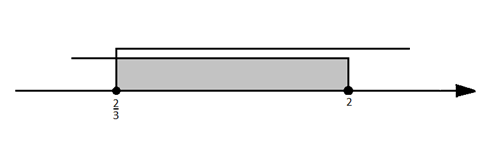
Więc:
![]()
W tym przedziale znajduje się 2 liczby całkowite. Pamiętaj, że nie liczymy
![]() , ponieważ nie jest liczbą całkowitą.
, ponieważ nie jest liczbą całkowitą.
Rozwiążmy nierówność
![]() . Wyrażenie w wartości bezwzględnej musi być mniejsze od 1 i większe od –1, zatem:
. Wyrażenie w wartości bezwzględnej musi być mniejsze od 1 i większe od –1, zatem:
![]() i
i
![]()
![]() i
i
![]()
![]() i
i
![]()
Zaznaczamy na osi liczbowej zbiory rozwiązań nierówności i ich część wspólną, która jest rozwiązaniem nierówności
![]() :
:

Więc:
![]()
W tym przedziale znajduje się 1 liczba całkowita. Pamiętaj, że nie liczymy 6 i 4, ponieważ przedział jest obustronnie otwarty.
Nierówność
![]() posiada najwięcej liczb całkowitych w swoim rozwiązaniu.
posiada najwięcej liczb całkowitych w swoim rozwiązaniu.

Ćwiczenie A.
92Przykład 1.
92Przykład 2.
93Przykład 3.
93Zadanie 1.
94Zadanie 2.
94Zadanie 3.
94Zadanie 4.
94Zadanie 5.
94Zadanie 6.
94Zadanie 2.
98Zadanie 16.
100Zadanie 17.
101Ćwiczenie A.
102Ćwiczenie B.
103Przykład 1.
103Zadanie 2.
104Zadanie 3.
104Zadanie 4.
104Zadanie 5.
104Zadanie 6.
105Zadanie 8.
105Zadanie 10.
105Zadanie 15.
106Przykład 1.
108Przykład 2.
108Przykład 3.
109Zadanie 1.
110Zadanie 3.
110Zadanie 4.
110Zadanie 5.
110Zadanie 6.
110Zadanie 7.
110Zadanie 9.
110Zadanie 10.
111Ćwiczenie B.
112Zadanie 1.
116Zadanie 2.
116Zadanie 3.
116Zadanie 4.
116Zadanie 7.
116Ćwiczenie A.
117Przykład 2.
119Przykład 3.
119Przykład 4.
120Przykład 5.
120Zadanie 3.
121Zadanie 4.
121Zadanie 5.
121Zadanie 6.
121Zadanie 7.
121Zadanie 8.
122Zadanie 9.
122Zadanie 10.
122Zadanie 11.
122Zadanie 13.
122Zadanie 14.
122Zadanie 16.
123Zadanie 20.
124Zadanie 21.
124Zadanie 23.
124Przykład 1.
126Przykład C.
127Zadanie 3.
127Zadanie 5.
128Zadanie 6.
128Zadanie 1.
130Zadanie 4.
130Zadanie 17.
132Zadanie 1.
134Zadanie 2.
134Zadanie 3.
134Zadanie 4.
134Zadanie 5.
134Zadanie 7.
134Zadanie 8.
134
