W tym zadaniu musisz rozwiązać układ równań
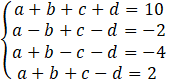
![]()
![]()
![]()
![]()
![]()
+
![]()
![]()
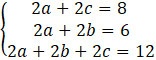
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
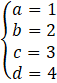

Oznaczmy równania jako:
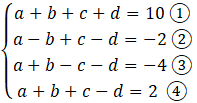
Aby zredukować ilość zmiennych zastosujemy metodę przeciwnych współczynników i porównamy ze sobą najpierw układ złożony z równania ① i ②.
![]() wyraz z b i d się redukują
wyraz z b i d się redukują
![]()
![]() oznaczamy równanie jako nr ⑤
oznaczamy równanie jako nr ⑤
Następnie porównujemy równania nr ① i
![]()
![]()
Aby zredukować ilość zmiennych zastosujemy metodę przeciwnych współczynników
![]() oznaczymy równanie jako nr ⑥.
oznaczymy równanie jako nr ⑥.
Teraz porównujemy równanie ① i
![]()
+
![]()
Aby zredukować ilość zmiennych zastosujemy metodę przeciwnych współczynników
![]() oznaczamy równanie jako nr ⑦.
oznaczamy równanie jako nr ⑦.
Powstał układ trzech równań ⑤, ⑥ i ⑦ z trzema niewiadomymi.
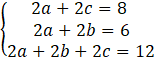
Ponownie stosujemy metodę przeciwnych współczynników, przy czym zauważamy, że porównując ze sobą równanie ⑤ i ⑦, zredukujemy od razu dwie zmienne:
![]()
![]()
![]()
![]()
![]()
Podstawiamy wartość b do równania nr ⑥.
![]()
![]()
![]()
![]()
![]()
Następnie wartości a i b podstawiamy do równania nr ⑦.
![]()
![]()
![]()
![]()
![]()
![]()
Do wzoru nr ① wstawiamy wartości a, b i c, żeby obliczyć d:
![]()
![]()
![]()
![]()

Ćwiczenie A.
92Przykład 1.
92Przykład 2.
93Przykład 3.
93Zadanie 1.
94Zadanie 2.
94Zadanie 3.
94Zadanie 4.
94Zadanie 5.
94Zadanie 6.
94Zadanie 2.
98Zadanie 16.
100Zadanie 17.
101Ćwiczenie A.
102Ćwiczenie B.
103Przykład 1.
103Zadanie 2.
104Zadanie 3.
104Zadanie 4.
104Zadanie 5.
104Zadanie 6.
105Zadanie 8.
105Zadanie 10.
105Zadanie 15.
106Przykład 1.
108Przykład 2.
108Przykład 3.
109Zadanie 1.
110Zadanie 3.
110Zadanie 4.
110Zadanie 5.
110Zadanie 6.
110Zadanie 7.
110Zadanie 9.
110Zadanie 10.
111Ćwiczenie B.
112Zadanie 1.
116Zadanie 2.
116Zadanie 3.
116Zadanie 4.
116Zadanie 7.
116Ćwiczenie A.
117Przykład 2.
119Przykład 3.
119Przykład 4.
120Przykład 5.
120Zadanie 3.
121Zadanie 4.
121Zadanie 5.
121Zadanie 6.
121Zadanie 7.
121Zadanie 8.
122Zadanie 9.
122Zadanie 10.
122Zadanie 11.
122Zadanie 13.
122Zadanie 14.
122Zadanie 16.
123Zadanie 20.
124Zadanie 21.
124Zadanie 23.
124Przykład 1.
126Przykład C.
127Zadanie 3.
127Zadanie 5.
128Zadanie 6.
128Zadanie 1.
130Zadanie 4.
130Zadanie 17.
132Zadanie 1.
134Zadanie 2.
134Zadanie 3.
134Zadanie 4.
134Zadanie 5.
134Zadanie 7.
134Zadanie 8.
134
