W tym zadaniu musisz wyznaczyć długości boków prostokątnej rabaty.
b–długość krótszego boku rabaty
a–długość dłuższego boku rabaty
a: b = 2: 1
a = 2b –stosunek boków
a > 0 ∧ b > 0
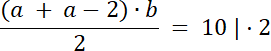
(2a–2)b = 20
2b(a–1) = 20
2b(2b–1) = 20
4b2–2b = 20|–20
4b2–2b–20 = 0
∆ = (–2)2–4∙4∙(–20)
∆ = 4 + 320
∆ = 324| √
√∆ = 18
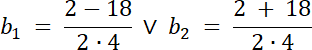
![]() , gdzie
, gdzie
![]() , więc:
, więc:
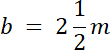
a = 2b
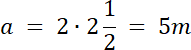
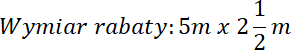

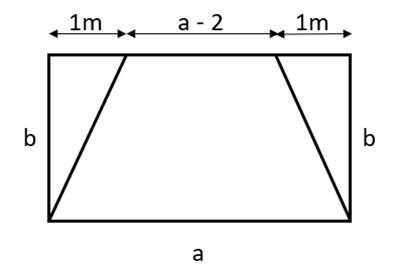
Na początek skorzystaj z rysunku pomocniczego, aby łatwiej określić wymiary rabaty. Dodatkowo zauważ, że stosunek boków wynosi 2 : 1, tj. jeden z boków jest 2 razy dłuższy od drugiego. Zauważ, że powierzchnia przeznaczona na róże ma kształt trapezu, a wzór na jego pole to 0,5(a + b)⋅h, gdzie: a i b–długości boków podstawy, h–wysokość opuszczona na podstawę trapezu. Następnie wstaw dane do wzoru, wyznacz wartość krótszego boku, pamiętaj, że długość musi być większa od zera. Na koniec wyznacz drugi bok prostokąta i podaj wymiar rabaty.

Ćwiczenie 1.
56Ćwiczenie 2.
57Ćwiczenie 4.
58Zadanie 1.
59Zadanie 2.
59Zadanie 3.
59Zadanie 4.
59Zadanie 5.
59Zadanie 6.
59Zadanie 7.
60Zadanie 8.
60Zadanie 9.
60Zadanie 1.
64Zadanie 2.
64Zadanie 3.
64Zadanie 4.
64Zadanie 5.
64Zadanie 6.
64Zadanie 7.
64Zadanie 8.
64Ćwiczenie 1.
65Ćwiczenie 3.
69Zadanie 1.
71Zadanie 2.
71Zadanie 3.
71Zadanie 4.
71Zadanie 5.
71Zadanie 6.
71Zadanie 7.
71Zadanie 8.
71Zadanie 9.
71Zadanie 10.
71Ćwiczenie 1.
72Zadanie 1.
74Zadanie 2.
74Zadanie 3.
74Zadanie 4.
74Zadanie 1.
81Zadanie 2.
81Zadanie 3.
82Zadanie 5.
82Ćwiczenie 1.
85Zadanie 4.
87Zadanie 8.
87Zadanie 1.
90Zadanie 2.
90Zadanie 3.
90Zadanie 4.
90Zadanie 5.
90Zadanie 6.
90Zadanie 7.
90Zadanie 8.
91Zadanie 9.
91Zadanie 10.
91Zadanie 11.
91Zadanie 12.
91Zadanie 13.
91Zadanie 17.
91Ćwiczenie 1.
92Zadanie 1.
92Zadanie 2.
92Zadanie 3.
93Zadanie 4.
93Zadanie 5.
93Ćwiczenie 1.
96Ćwiczenie 2.
96Zadanie 1.
96Zadanie 2.
97Zadanie 3.
97Zadanie 4.
97Zadanie 5.
97Zadanie 6.
97Zadanie 7.
97Zadanie 8.
97Zadanie 9.
97Zadanie 12.
103Zadanie 13.
103Zadanie 14.
103Zadanie 17.
103Zadanie 18.
103Zadanie 19.
103Zadanie 21.
103
