W tym zadaniu musisz rozwiązać nierówność kwadratową.
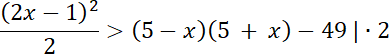
(2x–1)2 > 2(5–x)(5 + x)–98
4x2–4x + 1 > 2(25–x2)–98
4x2–4x + 1 > 50–2x2–98
4x2–4x + 1 >–2x2–48 | + 2x2 + 48
6x2–4x + 49 > 0
∆ = (–4)2–4∙6∙49
∆ = 16–1179 ⇔ ∆ < 0,
Wyznacznik jest mniejszy od zera, nierówność nie posiada miejsc zerowych.
Ramiona paraboli skierowane są do góry, współczynnik kierunkowy jest większy od zera więc:
6x2–4x + 49 > 0 ⇔ x ⋲ R

W pierwszym kroku wymnóż nierówność przez liczbę 2, aby pozbyć się zapisu ułamkowego. Następnie przenieś wszystko na jedną stronę nierówności i pogrupuj wyrażenia, a potem wyznacz wartość wyznacznika dla tej nierówności kwadratowej. Wyznacznik jest mniejszy od zera, a ramiona paraboli skierowane są do góry. Współczynnik kierunkowy jest większy od zera, więc nierówność jest spełniona dla każdej liczby rzeczywistej.

Ćwiczenie 1.
56Ćwiczenie 2.
57Ćwiczenie 4.
58Zadanie 1.
59Zadanie 2.
59Zadanie 3.
59Zadanie 4.
59Zadanie 5.
59Zadanie 6.
59Zadanie 7.
60Zadanie 8.
60Zadanie 9.
60Zadanie 1.
64Zadanie 2.
64Zadanie 3.
64Zadanie 4.
64Zadanie 5.
64Zadanie 6.
64Zadanie 7.
64Zadanie 8.
64Ćwiczenie 1.
65Ćwiczenie 3.
69Zadanie 1.
71Zadanie 2.
71Zadanie 3.
71Zadanie 4.
71Zadanie 5.
71Zadanie 6.
71Zadanie 7.
71Zadanie 8.
71Zadanie 9.
71Zadanie 10.
71Ćwiczenie 1.
72Zadanie 1.
74Zadanie 2.
74Zadanie 3.
74Zadanie 4.
74Zadanie 1.
81Zadanie 2.
81Zadanie 3.
82Zadanie 5.
82Ćwiczenie 1.
85Zadanie 4.
87Zadanie 8.
87Zadanie 1.
90Zadanie 2.
90Zadanie 3.
90Zadanie 4.
90Zadanie 5.
90Zadanie 6.
90Zadanie 7.
90Zadanie 8.
91Zadanie 9.
91Zadanie 10.
91Zadanie 11.
91Zadanie 12.
91Zadanie 13.
91Zadanie 17.
91Ćwiczenie 1.
92Zadanie 1.
92Zadanie 2.
92Zadanie 3.
93Zadanie 4.
93Zadanie 5.
93Ćwiczenie 1.
96Ćwiczenie 2.
96Zadanie 1.
96Zadanie 2.
97Zadanie 3.
97Zadanie 4.
97Zadanie 5.
97Zadanie 6.
97Zadanie 7.
97Zadanie 8.
97Zadanie 9.
97Zadanie 12.
103Zadanie 13.
103Zadanie 14.
103Zadanie 17.
103Zadanie 18.
103Zadanie 19.
103Zadanie 21.
103
