W tym zadaniu należy obliczyć jaką największą i najmniejszą wartość posiada wyrażenie x2 + 4x + 5, w przedziale, gdzie x ⋲ <–3, 1>.
x2 + 4x + 5
f(x) = x2 + 4x + 5, gdzie W–wierzchołek kwadratowy i W(p, q)
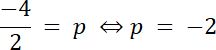
Dla x = –2, wyrażenie osiąga wartość minimalną, a–2 ⋲ <–3, 1>, więc
W(–2) = (–2)2 + 4(–2) + 5
W(–2) = 4–8 + 5
W(–2) = 1
Wartość maksymalna to punkt x najdalej oddalony od x = –2, więc
ymax = f(1)
f(1) = 12 + 4∙1 + 5
f(1) = 10

W pierwszym kroku wyznacz wierzchołek paraboli funkcji f i sprawdź, czy znajduje się on w przedziale <–3,1>. Wierzchołek paraboli: x = –2 i–2 ⋲<–3, 1>, a ramiona paraboli skierowane są do góry, więc ymin = f(–2), ymax funkcja osiąga dla x, który jest najbardziej oddalony od wierzchołka paraboli, czy dla punktu x = 1.

Ćwiczenie 1.
56Ćwiczenie 2.
57Ćwiczenie 4.
58Zadanie 1.
59Zadanie 2.
59Zadanie 3.
59Zadanie 4.
59Zadanie 5.
59Zadanie 6.
59Zadanie 7.
60Zadanie 8.
60Zadanie 9.
60Zadanie 1.
64Zadanie 2.
64Zadanie 3.
64Zadanie 4.
64Zadanie 5.
64Zadanie 6.
64Zadanie 7.
64Zadanie 8.
64Ćwiczenie 1.
65Ćwiczenie 3.
69Zadanie 1.
71Zadanie 2.
71Zadanie 3.
71Zadanie 4.
71Zadanie 5.
71Zadanie 6.
71Zadanie 7.
71Zadanie 8.
71Zadanie 9.
71Zadanie 10.
71Ćwiczenie 1.
72Zadanie 1.
74Zadanie 2.
74Zadanie 3.
74Zadanie 4.
74Zadanie 1.
81Zadanie 2.
81Zadanie 3.
82Zadanie 5.
82Ćwiczenie 1.
85Zadanie 4.
87Zadanie 8.
87Zadanie 1.
90Zadanie 2.
90Zadanie 3.
90Zadanie 4.
90Zadanie 5.
90Zadanie 6.
90Zadanie 7.
90Zadanie 8.
91Zadanie 9.
91Zadanie 10.
91Zadanie 11.
91Zadanie 12.
91Zadanie 13.
91Zadanie 17.
91Ćwiczenie 1.
92Zadanie 1.
92Zadanie 2.
92Zadanie 3.
93Zadanie 4.
93Zadanie 5.
93Ćwiczenie 1.
96Ćwiczenie 2.
96Zadanie 1.
96Zadanie 2.
97Zadanie 3.
97Zadanie 4.
97Zadanie 5.
97Zadanie 6.
97Zadanie 7.
97Zadanie 8.
97Zadanie 9.
97Zadanie 12.
103Zadanie 13.
103Zadanie 14.
103Zadanie 17.
103Zadanie 18.
103Zadanie 19.
103Zadanie 21.
103
