W tym zadaniu należy zapisać liczbę 80 w taki sposób, aby suma kwadratów tych dwóch liczb była najmniejsza.
h = x–pierwsza liczna
g = x + 80–druga liczba (różnica tych liczb jest równa 80)
f(x) = h2 + g2
f(x) = x2 + (x + 80)2
f(x)⇒ min
f(x) = x2 + (x2 + 160x + 6400)
f(x) = 2x2 + 160x + 6400
a = 2 i a > 0, więc f(x) = ymin dla wierzchołka funkcji, gdzie W(p, q)
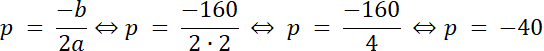
pierwsza liczba h = x⇒ h = –40
druga liczba g = x + 80⇒ g = –40 + 80⇒ g = 40

Jako pierwszą liczbę ustalamy liczbę h, gdzie h = x a drugą g, gdzie g = x + 80, ponieważ różnica tych liczb jest równa 80. Wyznacz wierzchołek funkcji kwadratowej, który określa wartość minimalną.

Ćwiczenie 1.
56Ćwiczenie 2.
57Ćwiczenie 4.
58Zadanie 1.
59Zadanie 2.
59Zadanie 3.
59Zadanie 4.
59Zadanie 5.
59Zadanie 6.
59Zadanie 7.
60Zadanie 8.
60Zadanie 9.
60Zadanie 1.
64Zadanie 2.
64Zadanie 3.
64Zadanie 4.
64Zadanie 5.
64Zadanie 6.
64Zadanie 7.
64Zadanie 8.
64Ćwiczenie 1.
65Ćwiczenie 3.
69Zadanie 1.
71Zadanie 2.
71Zadanie 3.
71Zadanie 4.
71Zadanie 5.
71Zadanie 6.
71Zadanie 7.
71Zadanie 8.
71Zadanie 9.
71Zadanie 10.
71Ćwiczenie 1.
72Zadanie 1.
74Zadanie 2.
74Zadanie 3.
74Zadanie 4.
74Zadanie 1.
81Zadanie 2.
81Zadanie 3.
82Zadanie 5.
82Ćwiczenie 1.
85Zadanie 4.
87Zadanie 8.
87Zadanie 1.
90Zadanie 2.
90Zadanie 3.
90Zadanie 4.
90Zadanie 5.
90Zadanie 6.
90Zadanie 7.
90Zadanie 8.
91Zadanie 9.
91Zadanie 10.
91Zadanie 11.
91Zadanie 12.
91Zadanie 13.
91Zadanie 17.
91Ćwiczenie 1.
92Zadanie 1.
92Zadanie 2.
92Zadanie 3.
93Zadanie 4.
93Zadanie 5.
93Ćwiczenie 1.
96Ćwiczenie 2.
96Zadanie 1.
96Zadanie 2.
97Zadanie 3.
97Zadanie 4.
97Zadanie 5.
97Zadanie 6.
97Zadanie 7.
97Zadanie 8.
97Zadanie 9.
97Zadanie 12.
103Zadanie 13.
103Zadanie 14.
103Zadanie 17.
103Zadanie 18.
103Zadanie 19.
103Zadanie 21.
103
