W tym zadaniu musisz ustalić dla jakiej wartości liczby a, zbiór rozwiązań nierówności to przedział liczbowy
![]()
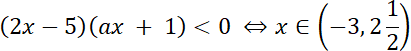
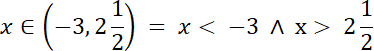
Aby nierówność była spełniona to:
![]() ,
,
![]()
![]()
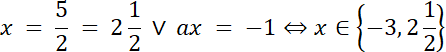
ax = –1 i x = –3
a(–3) = –1 / (–3)
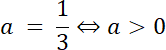

Na początku zauważ, że parabola musi mieć ramiona skierowane do góry, aby rozwiązanie nierówności mieściło się w przedziale podanym w treści zadania, więc a > 0. Następnie, przyrównaj nierówność do zera, aby wyznaczyć krańce przedziału, dla których nierówność jest prawdziwa. Zauważ, że jedną wartość liczbową wyznaczyć możesz z wyrażenia: 2x–5 = 0. Kolejną, gdzie x = –3, możesz wyznaczyć z drugiego wyrażenia: ax + 1. Po podstawieniu otrzymasz liczbę a. Jako że a > 0, to dla tej nierówności istnieje liczba a, dla której zbiorem rozwiązań nierówności jest przedział podany w treści zadania.

Ćwiczenie 1.
56Ćwiczenie 2.
57Ćwiczenie 4.
58Zadanie 1.
59Zadanie 2.
59Zadanie 3.
59Zadanie 4.
59Zadanie 5.
59Zadanie 6.
59Zadanie 7.
60Zadanie 8.
60Zadanie 9.
60Zadanie 1.
64Zadanie 2.
64Zadanie 3.
64Zadanie 4.
64Zadanie 5.
64Zadanie 6.
64Zadanie 7.
64Zadanie 8.
64Ćwiczenie 1.
65Ćwiczenie 3.
69Zadanie 1.
71Zadanie 2.
71Zadanie 3.
71Zadanie 4.
71Zadanie 5.
71Zadanie 6.
71Zadanie 7.
71Zadanie 8.
71Zadanie 9.
71Zadanie 10.
71Ćwiczenie 1.
72Zadanie 1.
74Zadanie 2.
74Zadanie 3.
74Zadanie 4.
74Zadanie 1.
81Zadanie 2.
81Zadanie 3.
82Zadanie 5.
82Ćwiczenie 1.
85Zadanie 4.
87Zadanie 8.
87Zadanie 1.
90Zadanie 2.
90Zadanie 3.
90Zadanie 4.
90Zadanie 5.
90Zadanie 6.
90Zadanie 7.
90Zadanie 8.
91Zadanie 9.
91Zadanie 10.
91Zadanie 11.
91Zadanie 12.
91Zadanie 13.
91Zadanie 17.
91Ćwiczenie 1.
92Zadanie 1.
92Zadanie 2.
92Zadanie 3.
93Zadanie 4.
93Zadanie 5.
93Ćwiczenie 1.
96Ćwiczenie 2.
96Zadanie 1.
96Zadanie 2.
97Zadanie 3.
97Zadanie 4.
97Zadanie 5.
97Zadanie 6.
97Zadanie 7.
97Zadanie 8.
97Zadanie 9.
97Zadanie 12.
103Zadanie 13.
103Zadanie 14.
103Zadanie 17.
103Zadanie 18.
103Zadanie 19.
103Zadanie 21.
103
