W tym zadaniu musisz określić dziedzinę funkcji f.
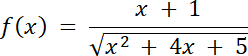
Dziedzina funkcji:
![]()
Wyznacz krańcowe wartości przedziału rozwiązań nierówności:
![]()
x2 + 4x + 5 = 0
∆ = (4)2–4∙5∙1
∆ = 16–20
∆ = –4 ⇔ ∆ < 0
g(x) = x2 + 4x + 5, a wierzchołek paraboli W(p, q)
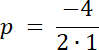
p = –2
g(–2) = q ⇔ g(–2) = (–2)2 + 4(–2) + 5
g(–2) = 4–8 + 5
g(–2) = 1, więc
Dziedzina funkcji f to x ⋲ R.

Wyrażenie pod pierwiastkiem jest zawsze większe od zera bądź równe zeru, jednak pamiętaj, że nie dzielimy przez zero, więc wyrażenie podane w mianowniku musi być większe od zera. Następnie wyznacz krańcowe wartości przedziału, przyrównując nierówność do zera. Wyróżnik osiąga wartość mniejszą od zera, więc równanie nie posiada miejsc zerowych. Dodatkowo ramiona paraboli skierowane są do góry, więc wyrażenie osiąga wartość minimalną dla wierzchołka paraboli, a wartość wierzchołka jest większa od zera, więc dziedzina funkcji f to x ⋲ R.

Ćwiczenie 1.
56Ćwiczenie 2.
57Ćwiczenie 4.
58Zadanie 1.
59Zadanie 2.
59Zadanie 3.
59Zadanie 4.
59Zadanie 5.
59Zadanie 6.
59Zadanie 7.
60Zadanie 8.
60Zadanie 9.
60Zadanie 1.
64Zadanie 2.
64Zadanie 3.
64Zadanie 4.
64Zadanie 5.
64Zadanie 6.
64Zadanie 7.
64Zadanie 8.
64Ćwiczenie 1.
65Ćwiczenie 3.
69Zadanie 1.
71Zadanie 2.
71Zadanie 3.
71Zadanie 4.
71Zadanie 5.
71Zadanie 6.
71Zadanie 7.
71Zadanie 8.
71Zadanie 9.
71Zadanie 10.
71Ćwiczenie 1.
72Zadanie 1.
74Zadanie 2.
74Zadanie 3.
74Zadanie 4.
74Zadanie 1.
81Zadanie 2.
81Zadanie 3.
82Zadanie 5.
82Ćwiczenie 1.
85Zadanie 4.
87Zadanie 8.
87Zadanie 1.
90Zadanie 2.
90Zadanie 3.
90Zadanie 4.
90Zadanie 5.
90Zadanie 6.
90Zadanie 7.
90Zadanie 8.
91Zadanie 9.
91Zadanie 10.
91Zadanie 11.
91Zadanie 12.
91Zadanie 13.
91Zadanie 17.
91Ćwiczenie 1.
92Zadanie 1.
92Zadanie 2.
92Zadanie 3.
93Zadanie 4.
93Zadanie 5.
93Ćwiczenie 1.
96Ćwiczenie 2.
96Zadanie 1.
96Zadanie 2.
97Zadanie 3.
97Zadanie 4.
97Zadanie 5.
97Zadanie 6.
97Zadanie 7.
97Zadanie 8.
97Zadanie 9.
97Zadanie 12.
103Zadanie 13.
103Zadanie 14.
103Zadanie 17.
103Zadanie 18.
103Zadanie 19.
103Zadanie 21.
103
