W tym zadaniu musisz rozwiązać nierówność kwadratową.
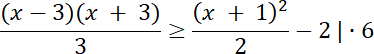
2(x–3)(x + 3) ≥ 3(x + 1)2–12
2(x2–9) ≥ 3(x + 1)2–12 |–3(x + 1)2 + 12
2(x2–9)–3(x + 1)2 + 12 ≥ 0
2x2–18–3(x2 + 2x + 1) + 12 ≥ 0
2x2–6–3x2–6x–3 ≥ 0
–x2–6x–9 ≥ 0 | /(–1)
x2 + 6x + 9 ≤ 0
(x + 3)2 ≤ 0 ⇔ (x + 3)2 = 0 | √ ⇔ x + 3 = 0 ⇔ x = –3 ⇔ x ⋲ R

W pierwszym kroku wymnóż nierówność przez liczbę 6, aby pozbyć się zapisu ułamkowego. Następnie przenieś wszystko na jedną stronę nierówności i pogrupuj wyrażenia. Zauważ, że zapisana nierówność x2 + 6x + 9 to rozpisany wzór skróconego mnożenia wyrażenia: (x + 3)2, a jak wiemy, wyrażenie podniesione do kwadratu jest zawsze większe od zera bądź równe zeru, więc nierówność jest prawdziwa tylko w jednym przypadku: (x + 3)2 = 0. Na koniec wyznaczasz wartość liczby x.

Ćwiczenie 1.
56Ćwiczenie 2.
57Ćwiczenie 4.
58Zadanie 1.
59Zadanie 2.
59Zadanie 3.
59Zadanie 4.
59Zadanie 5.
59Zadanie 6.
59Zadanie 7.
60Zadanie 8.
60Zadanie 9.
60Zadanie 1.
64Zadanie 2.
64Zadanie 3.
64Zadanie 4.
64Zadanie 5.
64Zadanie 6.
64Zadanie 7.
64Zadanie 8.
64Ćwiczenie 1.
65Ćwiczenie 3.
69Zadanie 1.
71Zadanie 2.
71Zadanie 3.
71Zadanie 4.
71Zadanie 5.
71Zadanie 6.
71Zadanie 7.
71Zadanie 8.
71Zadanie 9.
71Zadanie 10.
71Ćwiczenie 1.
72Zadanie 1.
74Zadanie 2.
74Zadanie 3.
74Zadanie 4.
74Zadanie 1.
81Zadanie 2.
81Zadanie 3.
82Zadanie 5.
82Ćwiczenie 1.
85Zadanie 4.
87Zadanie 8.
87Zadanie 1.
90Zadanie 2.
90Zadanie 3.
90Zadanie 4.
90Zadanie 5.
90Zadanie 6.
90Zadanie 7.
90Zadanie 8.
91Zadanie 9.
91Zadanie 10.
91Zadanie 11.
91Zadanie 12.
91Zadanie 13.
91Zadanie 17.
91Ćwiczenie 1.
92Zadanie 1.
92Zadanie 2.
92Zadanie 3.
93Zadanie 4.
93Zadanie 5.
93Ćwiczenie 1.
96Ćwiczenie 2.
96Zadanie 1.
96Zadanie 2.
97Zadanie 3.
97Zadanie 4.
97Zadanie 5.
97Zadanie 6.
97Zadanie 7.
97Zadanie 8.
97Zadanie 9.
97Zadanie 12.
103Zadanie 13.
103Zadanie 14.
103Zadanie 17.
103Zadanie 18.
103Zadanie 19.
103Zadanie 21.
103
