W tym zadaniu należy wyznaczyć wartości wszystkie argumenty x, dla których funkcja f przyjmuje wartość 7.
Oś symetrii ⇔ Oś OX dla x + 2 = 0 ⇔ x = –2
Argument wierzchołka funkcji f, x = –2 ⇔ W(–2, q)
Funkcja przecina oś OY w punkcie o rzędnej 7 ⇔ do wykresu należy punkt: (0, 7)
f(x) = 7 ⇔ x ⋲ {x1, 0}
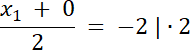
x1 + 0 = –4 ⇔ x1 = –4
f(x) = 7 ⇔ x ⋲ {–4, 0}

Z treści zadania wiemy, gdzie znajduje się wierzchołek funkcji (funkcji kwadratowej f jest symetryczny względem prostej x + 2 = 0, więc wierzchołkiem jest x = 2, oraz znamy jeden z dwóch argumentów, dla których funkcja f przyjmuje wartość 7 (0,7). Wystarczy zauważyć, że środek odcinka dwóch punktów paraboli posiadających wartość 7, prosta: x = –2, więc skorzystaj ze wzoru na środek odcinka, aby wyznaczyć drugi argument.

Ćwiczenie 1.
56Ćwiczenie 2.
57Ćwiczenie 4.
58Zadanie 1.
59Zadanie 2.
59Zadanie 3.
59Zadanie 4.
59Zadanie 5.
59Zadanie 6.
59Zadanie 7.
60Zadanie 8.
60Zadanie 9.
60Zadanie 1.
64Zadanie 2.
64Zadanie 3.
64Zadanie 4.
64Zadanie 5.
64Zadanie 6.
64Zadanie 7.
64Zadanie 8.
64Ćwiczenie 1.
65Ćwiczenie 3.
69Zadanie 1.
71Zadanie 2.
71Zadanie 3.
71Zadanie 4.
71Zadanie 5.
71Zadanie 6.
71Zadanie 7.
71Zadanie 8.
71Zadanie 9.
71Zadanie 10.
71Ćwiczenie 1.
72Zadanie 1.
74Zadanie 2.
74Zadanie 3.
74Zadanie 4.
74Zadanie 1.
81Zadanie 2.
81Zadanie 3.
82Zadanie 5.
82Ćwiczenie 1.
85Zadanie 4.
87Zadanie 8.
87Zadanie 1.
90Zadanie 2.
90Zadanie 3.
90Zadanie 4.
90Zadanie 5.
90Zadanie 6.
90Zadanie 7.
90Zadanie 8.
91Zadanie 9.
91Zadanie 10.
91Zadanie 11.
91Zadanie 12.
91Zadanie 13.
91Zadanie 17.
91Ćwiczenie 1.
92Zadanie 1.
92Zadanie 2.
92Zadanie 3.
93Zadanie 4.
93Zadanie 5.
93Ćwiczenie 1.
96Ćwiczenie 2.
96Zadanie 1.
96Zadanie 2.
97Zadanie 3.
97Zadanie 4.
97Zadanie 5.
97Zadanie 6.
97Zadanie 7.
97Zadanie 8.
97Zadanie 9.
97Zadanie 12.
103Zadanie 13.
103Zadanie 14.
103Zadanie 17.
103Zadanie 18.
103Zadanie 19.
103Zadanie 21.
103
