W tym zadaniu musisz znaleźć wszystkie liczby naturalne dwucyfrowe, których suma cyfr wynosi 6, a iloczyn tej liczby i cyfry jej dziesiątek będzie mniejszy od 120.
x–cyfra jedności liczby naturalnej dwucyfrowej
(6–x)–cyfra dziesiątek liczby naturalnej
10(6–x) + x = 60–10x + x = 60–9x ⇔ liczba dwucyfrowa naturalna
x ⋲ N∧ 0 ≤ x ≤ 9,
0 ≤ x ≤ 9 |⋅ (–1)
–9 ≤–x ≤ 0 | + 6
–3 ≤ 6–x ≤ 6, więc:
x ⋲ N∧ 0 ≤ x ≤ 9 ∧ –3 ≤ 6–x ≤ 6
(60–9x)(6–x) < 120
360–60x–54x + 9x2 < 120 |–120
9x2–114x + 240 < 0
∆ = (–114)2–4∙9∙240
∆ = 12996–8640
∆ = 4356 | √
√∆ = 66
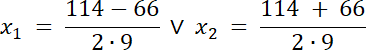
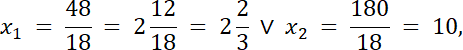
Ramiona paraboli skierowane są do góry, więc:
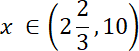
![]()
Te liczby to: 33, 24, 15

W pierwszym kroku musisz dobrze zapisać szukane wartości, a następnie dokładnie określić dziedzinę rozwiązań liczby x. Następnie, na podstawie treści zadania zapisać nierówność, wyznaczyć zbiór rozwiązań, porównać go ze zbiorem wyznaczonym na początku zadania. W kolejnym kroku wyznacz część wspólną tych zbiorów. Na koniec zapisz szukane liczby.

Ćwiczenie 1.
56Ćwiczenie 2.
57Ćwiczenie 4.
58Zadanie 1.
59Zadanie 2.
59Zadanie 3.
59Zadanie 4.
59Zadanie 5.
59Zadanie 6.
59Zadanie 7.
60Zadanie 8.
60Zadanie 9.
60Zadanie 1.
64Zadanie 2.
64Zadanie 3.
64Zadanie 4.
64Zadanie 5.
64Zadanie 6.
64Zadanie 7.
64Zadanie 8.
64Ćwiczenie 1.
65Ćwiczenie 3.
69Zadanie 1.
71Zadanie 2.
71Zadanie 3.
71Zadanie 4.
71Zadanie 5.
71Zadanie 6.
71Zadanie 7.
71Zadanie 8.
71Zadanie 9.
71Zadanie 10.
71Ćwiczenie 1.
72Zadanie 1.
74Zadanie 2.
74Zadanie 3.
74Zadanie 4.
74Zadanie 1.
81Zadanie 2.
81Zadanie 3.
82Zadanie 5.
82Ćwiczenie 1.
85Zadanie 4.
87Zadanie 8.
87Zadanie 1.
90Zadanie 2.
90Zadanie 3.
90Zadanie 4.
90Zadanie 5.
90Zadanie 6.
90Zadanie 7.
90Zadanie 8.
91Zadanie 9.
91Zadanie 10.
91Zadanie 11.
91Zadanie 12.
91Zadanie 13.
91Zadanie 17.
91Ćwiczenie 1.
92Zadanie 1.
92Zadanie 2.
92Zadanie 3.
93Zadanie 4.
93Zadanie 5.
93Ćwiczenie 1.
96Ćwiczenie 2.
96Zadanie 1.
96Zadanie 2.
97Zadanie 3.
97Zadanie 4.
97Zadanie 5.
97Zadanie 6.
97Zadanie 7.
97Zadanie 8.
97Zadanie 9.
97Zadanie 12.
103Zadanie 13.
103Zadanie 14.
103Zadanie 17.
103Zadanie 18.
103Zadanie 19.
103Zadanie 21.
103
