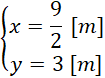Suma obwodów klatek = 6y + 4x
![]()
![]()
![]()
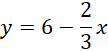
Pole jednej klatki = x∙y
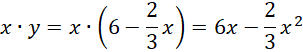
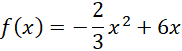
f(x) przyjmuje wartość najmniejszą dla argumentu wierzchołka, czyli dla p.
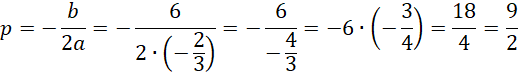
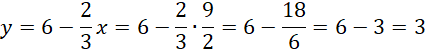
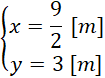

Zapisz obwód wszystkich klatek , uwzględniając ściany między klatkami.
Suma obwodów klatek = 6y + 4x
Z polecenia wiesz, że suma obwodów jest równa 36 metrów.
![]()
Wylicz z powstałego równania y.
![]()
![]()
![]()
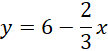
Zapisz wzór na pole jednej klatki. Zamiast y podstaw wyliczoną zależność między x i y.
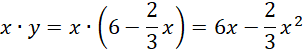
Powstała zależność opisująca pole klatki w zależności od x. Oznacz ją jako f(x).
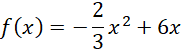
Funkcja f jest funkcją kwadratową. Współczynnik przy drugiej potędze niewiadomej jest ujemny, więc wykres tej funkcji ma ramiona skierowane w dół. Oznacza to, że jest punkt, który znajduje się najwyżej (reprezentuje największe pole) – jest to wierzchołek paraboli będącej wykresem tej funkcji.
x wierzchołka, czyli p, jest x dla którego klatka ma największe pole. Wylicz p korzystając ze wzoru.
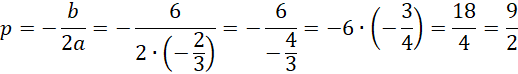
Wróć do zależności y od x. Podstaw wyliczonego x, aby dostać y
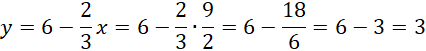
Zapisz wynik