Udowodnij, że środki kolejnych boków każdego czworokąta tworzą wierzchołki równoległoboku.
|AK| = |KD|
|DN| = |NC|
|CM| = |MB|
|BL| = |LA|
Zauważamy, że:
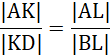
Stąd, na mocy twierdzenia odwrotnego do twierdzenia Talesa:
![]()
Zauważamy, że:
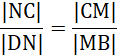
Stąd, na mocy twierdzenia odwrotnego do twierdzenia Talesa:
![]()
Z (*) i (**) wynika, że:
![]()
Analogicznie można rozpisać, że para odcinków |KN| i |ML| są parami równoległe.
Więc czworokąt KLMN ma dwie pary boków równoległych więc jest równoległobokiem – c.n.d.


Ćwiczenie 1
202Ćwiczenie 2
202Ćwiczenie 4
202Zadanie 9.1
203Zadanie 9.4
203Zadanie 9.7
203Zadanie 9.9
203Ćwiczenie 5
205Ćwiczenie 6
206Ćwiczenie 8
207Ćwiczenie 9
208Zadanie 9.11
209Zadanie 9.19
209Ćwiczenie 11
211Ćwiczenie 12
212Ćwiczenie 14
214Zadanie 9.23
214Ćwiczenie 15
215Ćwiczenie 18
217Ćwiczenie 20
217Ćwiczenie 21
217Ćwiczenie 22
217Ćwiczenie 23
218Ćwiczenie 25
219Zadanie 9.32
219Zadanie 9.34
220Zadanie 9.35
220Zadanie 9.36
220Zadanie 9.37
220Zadanie 9.39
221Zadanie 9.40
221Ćwiczenie 27
222Ćwiczenie 28
223Zadanie 9.42
225Zadanie 9.45
225Zadanie 9.46
225
