Musisz udowodnić przystawanie podanych trójkątów.
Trójkąt ABC jest trójkątem równoramiennym, więc:
![]()
Poprowadzone odcinki AE oraz BD zawierają się w dwusiecznych kątów przy podstawie AB, więc:
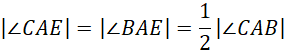
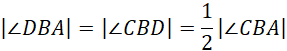
Niech:
![]()
Wtedy kąt |∠AOB| wynosi:
![]()
Stąd wynika, że:
![]()
Z własności trójkątów możemy obliczyć również:
![]()
Podsumowując:
![]()
![]()
![]()
Stąd możemy ustalić, że trójkąty ABE i ABD są przystające z cechy kąt – kąt – kąt.


Ćwiczenie 1
202Ćwiczenie 2
202Ćwiczenie 4
202Zadanie 9.1
203Zadanie 9.4
203Zadanie 9.7
203Zadanie 9.9
203Ćwiczenie 5
205Ćwiczenie 6
206Ćwiczenie 8
207Ćwiczenie 9
208Zadanie 9.11
209Zadanie 9.19
209Ćwiczenie 11
211Ćwiczenie 12
212Ćwiczenie 14
214Zadanie 9.23
214Ćwiczenie 15
215Ćwiczenie 18
217Ćwiczenie 20
217Ćwiczenie 21
217Ćwiczenie 22
217Ćwiczenie 23
218Ćwiczenie 25
219Zadanie 9.32
219Zadanie 9.34
220Zadanie 9.35
220Zadanie 9.36
220Zadanie 9.37
220Zadanie 9.39
221Zadanie 9.40
221Ćwiczenie 27
222Ćwiczenie 28
223Zadanie 9.42
225Zadanie 9.45
225Zadanie 9.46
225
