Oblicz, jaką długość ma przeciwprostokątna AB, wiedząc, że długość AC wynosi 12.
Przeciwprostokątna |AB| może wynosić 24 lub 8√3.

Niech przeciwprostokątna |AB|:
![]()
Wtedy wysokość |CD| dzieli przeciwprostokątną na dwa odcinki |AD| i |DB| o długości x i 3x.
Zgodnie z twierdzeniem o wysokości w trójkącie prostokątnym:
![]()
Istnieją dwa rozwiązania tego zadania:
I rozwiązanie)
Bok |AC| jest krótszą przyprostokątną trójkąta ABC:
Wtedy z tw. Pitagorasa:
![]()
![]()
Stąd wynika, że:
![]()
II rozwiązanie)
Bok |AC| jest dłuższą przyprostokątną trójkąta ABC:
Wtedy z tw. Pitagorasa:
![]()
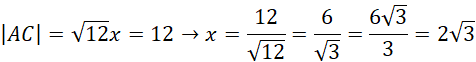
Stąd wynika, że:
![]()

Ćwiczenie 1
202Ćwiczenie 2
202Ćwiczenie 4
202Zadanie 9.1
203Zadanie 9.4
203Zadanie 9.7
203Zadanie 9.9
203Ćwiczenie 5
205Ćwiczenie 6
206Ćwiczenie 8
207Ćwiczenie 9
208Zadanie 9.11
209Zadanie 9.19
209Ćwiczenie 11
211Ćwiczenie 12
212Ćwiczenie 14
214Zadanie 9.23
214Ćwiczenie 15
215Ćwiczenie 18
217Ćwiczenie 20
217Ćwiczenie 21
217Ćwiczenie 22
217Ćwiczenie 23
218Ćwiczenie 25
219Zadanie 9.32
219Zadanie 9.34
220Zadanie 9.35
220Zadanie 9.36
220Zadanie 9.37
220Zadanie 9.39
221Zadanie 9.40
221Ćwiczenie 27
222Ćwiczenie 28
223Zadanie 9.42
225Zadanie 9.45
225Zadanie 9.46
225
