W tym zadaniu wyznacz równania okręgu przechodzącego przez punkty A i B, którego środek należy do prostej l.
A(–2, 2), B(2, 4), l: y = 1
![]() = (0, 3)
= (0, 3)
a =
![]()
![]() · a2 = –1 / · 2
· a2 = –1 / · 2
a2 = –2
k: y = –2x + b
3 = – 2 · 0 + b
b = 3
y = –2x + 3
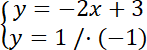
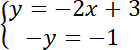
0 = –2x + 2
2x = 2 / :2
x = 1
y = 1
Zatem S(1, 1).
r = |SA| =
![]()
Równanie okręgu ma postać: (x – 1)2 + (y – 1)2 = 10

Odcinek AB to cięciwa okręgu. Wyznaczamy środek AB:
![]() = (0, 3)
= (0, 3)
Obliczamy współczynnik kierunkowy prostej AB:
a =
![]()
Symetralna odcinka AB jest do niej prostopadła, więc:
![]() · a2 = –1 / · 2
· a2 = –1 / · 2
a2 = –2
Jej równanie ma postać:
k: y = –2x + b
Do prostej k tej należy punkt P(0, 3), zatem:
3 = – 2 · 0 + b
b = 3
Zatem prosta k ma postać:
y = –2x + 3
Środek okręgu jest punktem przecięcia prostej k i prostej l, wyznaczamy te współrzędne:
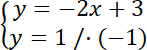
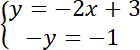
0 = –2x + 2
2x = 2 / :2
x = 1
y = 1
Zatem S(1, 1).
Obliczamy promień okręgu:
r = |SA| =
![]()
Równanie okręgu ma postać: (x – 1)2 + (y – 1)2 = 10
Symetralna to prosta prostopadła do odcinka, która przechodzi przez środek tego odcinka. W celu wyznaczenia współczynnika kierunkowego prostej y = ax + b przechodzącej przez punkty (x1, y1) i (x2, y2), gdzie x1≠ x2, wykorzystaj wzór
![]() . Skorzystaj ze wzoru na środek odcinka AB o końcach w punktach A(x1, y1) i B(x2, y2), który wygląda następująco:
. Skorzystaj ze wzoru na środek odcinka AB o końcach w punktach A(x1, y1) i B(x2, y2), który wygląda następująco:
![]() . Okrąg, którego środek znajduje się w punkcie (a, i promieniu r > 0 jest zbiorem wszystkich punktów na płaszczyźnie, których współrzędne (x, y) spełniają równanie: (x – a)2 + (y – b)2 = r2. W celu obliczenia odległości między punktami S(xp, yp) i A(xs, ys) skorzystaj z następującego wzoru: |SA| =
. Okrąg, którego środek znajduje się w punkcie (a, i promieniu r > 0 jest zbiorem wszystkich punktów na płaszczyźnie, których współrzędne (x, y) spełniają równanie: (x – a)2 + (y – b)2 = r2. W celu obliczenia odległości między punktami S(xp, yp) i A(xs, ys) skorzystaj z następującego wzoru: |SA| =
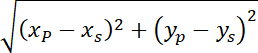 .
.

Zadanie 1.
54Zadanie 2.
54Zadanie 4.
54Zadanie 5.
54Ćwiczenie 1.
55Ćwiczenie 4.
56Ćwiczenie 5.
56Zadanie 2.
56Zadanie 3.
56Zadanie 4.
56Zadanie 5.
56Zadanie 6.
56Zadanie 7.
56Zadanie 10.
56Zadanie 12.
56Zadanie 13.
56Ćwiczenie 1.
58Ćwiczenie 2.
58Ćwiczenie 3.
59Zadanie 1.
59Zadanie 2.
59Zadanie 3.
59Zadanie 5.
59Zadanie 6.
60Zadanie 8.
60Zadanie 9.
60Zadanie 10.
60Zadanie 11.
60Zadanie 13.
60Zadanie 14.
60Zadanie 2.
61Zadanie 3.
61Zadanie 4.
61Zadanie 5.
61Zadanie 6.
61Zadanie 7.
61Ćwiczenie 1.
62Ćwiczenie 2.
63Ćwiczenie 3.
63Ćwiczenie 5.
64Zadanie 1.
64Zadanie 4.
64Zadanie 5.
65Zadanie 6.
65Zadanie 7.
65Zadanie 8.
65Zadanie 9.
65Zadanie 10.
65Zadanie 11.
65Zadanie 1.
66Ćwiczenie 1.
67Ćwiczenie 3.
67Ćwiczenie 4.
68Ćwiczenie 5.
68Ćwiczenie 6.
69Ćwiczenie 7.
69Ćwiczenie 8.
69Ćwiczenie 9.
69Zadanie 1.
70Zadanie 2.
70Zadanie 3.
70Zadanie 5.
70Zadanie 6.
70Zadanie 7.
70Zadanie 9.
70Zadanie 10.
70Zadanie 11.
70Zadanie 12.
70Zadanie 13.
70Zadanie 15.
71Ćwiczenie 1.
72Ćwiczenie 2.
73Zadanie 1.
74Zadanie 2.
74Zadanie 3.
74Zadanie 6.
74Zadanie 1.
75Ćwiczenie 1.
76Ćwiczenie 2.
77Ćwiczenie 3.
77Zadanie 1.
78Zadanie 2.
78Zadanie 3.
78Zadanie 5.
78Zadanie 6.
78Ćwiczenie 1.
80Ćwiczenie 2.
81Ćwiczenie 3.
81Ćwiczenie 4.
81Zadanie 1.
82Zadanie 2.
82Zadanie 3.
82Zadanie 4.
82Zadanie 5.
82Zadanie 6.
82Zadanie 7.
82Zadanie 8.
82Ćwiczenie 1.
83Ćwiczenie 2.
83Zadanie 1.
85Zadanie 3.
85Zadanie 4.
85Zadanie 5.
85Zadanie 6.
85Zadanie 7.
85Ćwiczenie 1.
86Ćwiczenie 2.
87Zadanie 1.
88Zadanie 5.
88Zadanie 6.
88Ćwiczenie 1.
89Ćwiczenie 2.
89Ćwiczenie 3.
90Ćwiczenie 4.
90Ćwiczenie 5.
91Ćwiczenie 6.
91Zadanie 1.
92Zadanie 5.
92Zadanie 6.
92Zadanie 7.
92Ćwiczenie 1.
93Ćwiczenie 3.
94Ćwiczenie 4.
94Ćwiczenie 5.
94Ćwiczenie 7.
94Zadanie 1.
95Zadanie 2.
95Zadanie 3.
95Zadanie 4.
96Zadanie 5.
96Zadanie 6.
95Zadanie 7.
96Zadanie 8.
96Zadanie 9.
96Ćwiczenie 1.
97Ćwiczenie 3.
98Ćwiczenie 4.
98Ćwiczenie 6.
99Ćwiczenie 7.
99Zadanie 1.
99Zadanie 2.
99Zadanie 4.
99Zadanie 7.
101Zadanie 8.
100Zadanie 9.
100Zadanie 1.
101Zadanie 2.
101Zadanie 3.
103Zadanie 4.
103Zadanie 1.
104Zadanie 2.
104Zadanie 3.
104Zadanie 4.
104Zadanie 5.
104Zadanie 6.
104Zadanie 7.
104Zadanie 8.
104Zadanie 9.
105Zadanie 10.
105Zadanie 11.
105Zadanie 12.
105Zadanie 13.
105Zadanie 14.
105Zadanie 1.
106Zadanie 2.
106Zadanie 3.
106Zadanie 4.
106Zadanie 5.
106Zadanie 6.
106Zadanie 7.
106Zadanie 8.
106Zadanie 9.
106Zadanie 11.
107Zadanie 12.
107Zadanie 13.
107Zadanie 14.
107Zadanie 15.
106Zadanie 16.
107
