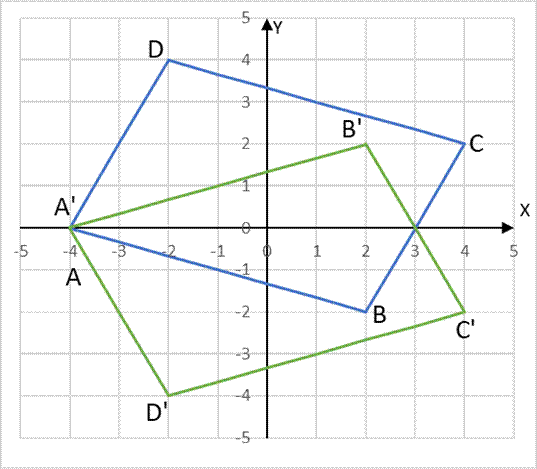
W tym zadaniu oblicz pole i obwód deltoidu będącego częścią wspólną tych równoległoboków oraz określ, ile punktów o obu współrzędnych całkowitych należy do tego deltoidu, wiedząc, ze równoległobok A’B’C’D’ jest symetryczny względem osi OX do równoległoboku o wierzchołkach A(–4,0), B(2,–2), C(4, 2) i D(–2, 4).
Obliczymy długość odcinka B’ (2, 2) od punktu P1(3, 0):
|BP1| =
![]()
Obliczymy długość odcinka B’ (2, 2) od punktu A’(–4, 0):
|BA’| =
![]()
Obliczymy długość odcinka B’ (2, 2) od punktu P2(2, 0):
|BP2| =
![]()
Odległość |A’P1| wynosi 7, co możemy odczytaj z powyższego wykresu.
Obw. = 2|BP1| + 2|BA’| = 2√5 + 4√10
Pole deltoidu składa się z dwóch pól trójkąta A’B’P1:
P = 2 (0,5 · |A’P1| · |B’P2|) = 2 · 0,5 · 7 · 2 = 14
Do deltoidu będącego częścią wspólną należy 18 punktów o współrzędnych całkowitych.

Równoległobok ABCD i równoległobok do niego symetryczny przedstaw na układzie współrzędnych, a następnie odczytaj punkty o obu współrzędnych całkowitych, które są częścią wspólną tych prostokątów. wyznaczyć długości potrzebnych nam boków do obliczenia pola i obwodu deltoidu ze wzoru na odległość między dwoma punktami. Punktem symetrycznym do punktu P(x, y) względem osi OX układu współrzędnych jest punkt P’(x, –y). W celu obliczenia odległości między punktami A(xa, ya) i b(xb, yb) skorzystaj z następującego wzoru: |AB| =
![]() . Liczby całkowite to wszystkie liczby naturalne oraz liczby przeciwne do nich np. –7, 7, –50, 50 itd. Obwód to suma długości wszystkich boków danej figury.
. Liczby całkowite to wszystkie liczby naturalne oraz liczby przeciwne do nich np. –7, 7, –50, 50 itd. Obwód to suma długości wszystkich boków danej figury.

Zadanie 1.
54Zadanie 2.
54Zadanie 4.
54Zadanie 5.
54Ćwiczenie 1.
55Ćwiczenie 4.
56Ćwiczenie 5.
56Zadanie 2.
56Zadanie 3.
56Zadanie 4.
56Zadanie 5.
56Zadanie 6.
56Zadanie 7.
56Zadanie 10.
56Zadanie 12.
56Zadanie 13.
56Ćwiczenie 1.
58Ćwiczenie 2.
58Ćwiczenie 3.
59Zadanie 1.
59Zadanie 2.
59Zadanie 3.
59Zadanie 5.
59Zadanie 6.
60Zadanie 8.
60Zadanie 9.
60Zadanie 10.
60Zadanie 11.
60Zadanie 13.
60Zadanie 14.
60Zadanie 2.
61Zadanie 3.
61Zadanie 4.
61Zadanie 5.
61Zadanie 6.
61Zadanie 7.
61Ćwiczenie 1.
62Ćwiczenie 2.
63Ćwiczenie 3.
63Ćwiczenie 5.
64Zadanie 1.
64Zadanie 4.
64Zadanie 5.
65Zadanie 6.
65Zadanie 7.
65Zadanie 8.
65Zadanie 9.
65Zadanie 10.
65Zadanie 11.
65Zadanie 1.
66Ćwiczenie 1.
67Ćwiczenie 3.
67Ćwiczenie 4.
68Ćwiczenie 5.
68Ćwiczenie 6.
69Ćwiczenie 7.
69Ćwiczenie 8.
69Ćwiczenie 9.
69Zadanie 1.
70Zadanie 2.
70Zadanie 3.
70Zadanie 5.
70Zadanie 6.
70Zadanie 7.
70Zadanie 9.
70Zadanie 10.
70Zadanie 11.
70Zadanie 12.
70Zadanie 13.
70Zadanie 15.
71Ćwiczenie 1.
72Ćwiczenie 2.
73Zadanie 1.
74Zadanie 2.
74Zadanie 3.
74Zadanie 6.
74Zadanie 1.
75Ćwiczenie 1.
76Ćwiczenie 2.
77Ćwiczenie 3.
77Zadanie 1.
78Zadanie 2.
78Zadanie 3.
78Zadanie 5.
78Zadanie 6.
78Ćwiczenie 1.
80Ćwiczenie 2.
81Ćwiczenie 3.
81Ćwiczenie 4.
81Zadanie 1.
82Zadanie 2.
82Zadanie 3.
82Zadanie 4.
82Zadanie 5.
82Zadanie 6.
82Zadanie 7.
82Zadanie 8.
82Ćwiczenie 1.
83Ćwiczenie 2.
83Zadanie 1.
85Zadanie 3.
85Zadanie 4.
85Zadanie 5.
85Zadanie 6.
85Zadanie 7.
85Ćwiczenie 1.
86Ćwiczenie 2.
87Zadanie 1.
88Zadanie 5.
88Zadanie 6.
88Ćwiczenie 1.
89Ćwiczenie 2.
89Ćwiczenie 3.
90Ćwiczenie 4.
90Ćwiczenie 5.
91Ćwiczenie 6.
91Zadanie 1.
92Zadanie 5.
92Zadanie 6.
92Zadanie 7.
92Ćwiczenie 1.
93Ćwiczenie 3.
94Ćwiczenie 4.
94Ćwiczenie 5.
94Ćwiczenie 7.
94Zadanie 1.
95Zadanie 2.
95Zadanie 3.
95Zadanie 4.
96Zadanie 5.
96Zadanie 6.
95Zadanie 7.
96Zadanie 8.
96Zadanie 9.
96Ćwiczenie 1.
97Ćwiczenie 3.
98Ćwiczenie 4.
98Ćwiczenie 6.
99Ćwiczenie 7.
99Zadanie 1.
99Zadanie 2.
99Zadanie 4.
99Zadanie 7.
101Zadanie 8.
100Zadanie 9.
100Zadanie 1.
101Zadanie 2.
101Zadanie 3.
103Zadanie 4.
103Zadanie 1.
104Zadanie 2.
104Zadanie 3.
104Zadanie 4.
104Zadanie 5.
104Zadanie 6.
104Zadanie 7.
104Zadanie 8.
104Zadanie 9.
105Zadanie 10.
105Zadanie 11.
105Zadanie 12.
105Zadanie 13.
105Zadanie 14.
105Zadanie 1.
106Zadanie 2.
106Zadanie 3.
106Zadanie 4.
106Zadanie 5.
106Zadanie 6.
106Zadanie 7.
106Zadanie 8.
106Zadanie 9.
106Zadanie 11.
107Zadanie 12.
107Zadanie 13.
107Zadanie 14.
107Zadanie 15.
106Zadanie 16.
107
