Malarz zamówił 14 pętli. Większe pędzle mają cenę 18 zł za sztukę, a mniejsze kosztują 12 zł. Jeśli jego zamówienie kosztowało 216 zł, oblicz ile kupił pędzli z każdego rodzaju.
x – ilość małych pędzli
y – ilość dużych pędzli
![]()
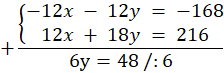
![]()
![]()
![]()
Malarz kupił 6 małych pędzli i 8 dużych.

Wiesz, że łącznie małych i dużych pędzli było 14, a więc ich suma wynosi 14, co zapisz jako x + y = 14. Cena małego pędzla wynosi 12zł, a więc ceny wszystkich małych pędzli zapisz jako 12x, z kolei cena dużego pędzla wynosi 18 zł, a więc ceny wszystkich dużych pędzli zapisz jako 18y. Łączna cena wszystkich pędzli wynosi 216 zł, ostatecznie więc równanie możesz zapisać jako 12x + 18y = 216. Pierwsze równanie pomnóż przez -12 w celu zrównania liczb x w obu równaniach, aby można było ten układ rozwiązać metodą przeciwnych współczynników. Po wykonaniu tego kroku dodaj do siebie równania stronami i wylicz y, pamiętając o zmianie znaków przy przenoszeniu na drugą stronę równania. Podstaw y do pierwszego równania w celu wyliczenia x.

Zadanie 1.
195Zadanie 4.
195Zadanie 2.
195Zadanie 1.
196Zadanie 2.
197Zadanie 2.
197Zadanie 4.
198Zadanie 1.
198Zadanie 2.
198Zadanie 1.
199Zadanie 1.
199Zadanie 2.
199Zadanie 4.
199Zadanie 7.
200Zadanie 1.
200Zadanie 4.
200Zadanie 1.
201Zadanie 2.
201Zadanie 1.
201Zadanie 2.
203Zadanie 3.
203Zadanie 1.
204Zadanie 2.
204Zadanie 3.
204Zadanie 4.
204Zadanie 5.
205Zadanie 2.
206Zadanie 1.
207Zadanie 5.
207Zadanie 1.
209Zadanie 4.
209Zadanie 1.
209Zadanie 2.
210Zadanie 5.
211Zadanie 6.
211Zadanie 2.
211Zadanie 3.
211Zadanie 4.
211Zadanie 5.
212Zadanie 2.
213Zadanie 3.
213Zadanie 4.
213Zadanie 4.
214Zadanie 1.
214Zadanie 4.
214Zadanie 4.
215Zadanie 3.
218Zadanie 4.
218Zadanie 2.
218Zadanie 3.
218Zadanie 1.
219Zadanie 4.
219Zadanie 2.
220Zadanie 3.
220Zadanie 4.
221Zadanie 1.
221Zadanie 2.
221
