Mając prostokąt ABCD leżący na okręgu o środku S i wiedząc, że bok LS trójkąta KLS jest równoległy do AD, a bok KS tego trójkąta jest równoległy do AB, skorzystaj z danych na rysunku i wyznacz wartość wyrażenia ![]()
![]()
![]()
![]()
![]()
![]()
![]()
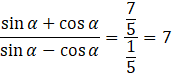

Wiedząc, że każdy wierzchołek prostokąta ABCD leży na okręgu, możesz wywnioskować, że odcinek SK to połowa dłuższego boku. Ponadto SB jest promieniem okręgu, o którym z rysunku możesz, zauważyć, że jest równy 5, zatem z faktu, że przekątne w prostokącie są równe, wynika, że ![]()

Zadanie 1.4.
317Zadanie 1.6.
318Zadanie 1.7.
318Zadanie 1.8.
318Zadanie 1.9.
318Zadanie 1.10.
318Zadanie 1.11.
318Zadanie 1.12.
318Zadanie 1.13.
319Zadanie 1.14.
319Zadanie 1.15.
319Zadanie 1.19.
319Zadanie 1.20.
319Zadanie 1.21.
319Zadanie 1.22.
320Zadanie 1.23.
320Zadanie 2.4.
325Zadanie 2.5.
325Zadanie 2.6.
325Zadanie 2.7.
326Zadanie 2.9.
326Zadanie 2.10.
326Zadanie 2.11.
326Zadanie 2.12.
326Zadanie 3.12.
332Zadanie 3.19.
333Zadanie 4.5.
339Zadanie 4.6.
339Zadanie 4.21.
341Zadanie 5.5.
350Zadanie 5.6.
351Zadanie 5.8.
351Zadanie 5.9.
351Zadanie 5.10.
351Zadanie 5.11.
351Zadanie 5.12.
351Zadanie 5.13.
351Zadanie 5.14.
351Zadanie 6.4.
356Zadanie 6.5.
356Zadanie 6.6.
356Zadanie 6.7.
356Zadanie 6.10.
356Zadanie 6.11.
356Zadanie 6.12.
356Zadanie 6.15.
356Zadanie 6.16.
356Zadanie 28.
362Zadanie 29.
362Zadanie 30.
362Zadanie 40.
363Zadanie 41.
361Zadanie 54.
364
