Matematyka 4. Zbiór zadań do liceów i techników. Zakres podstawowy

Podręcznik, Wydawnictwo: OE Pazdro

Zadanie 1.18 - strona 8

Udowodnij , że jeśli $\text{[math]}$ i $\text{[math]}$ , to $\text{[math]}$ .

$\text{[math]}$

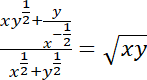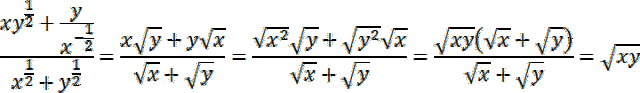
Lewą stronę podanego równania doprowadź do prawej, aby to zrobić skorzystaj z tego, że potęgę o wykładniku wymiernym można zapisać za pomocą pierwiastka: $\text{[math]}$ .

Zadanie 5, strona 73, Matematyka z plusem. Klasa 5. Zeszyt Ćwiczeń – rozwiązania i odpowiedzi

Zadanie Co było na lekcji 2, strona 103, Matematyka. Klasa 5. Zeszyt ćwiczeń część 1 - rozwiązania i odpowiedzi.

Zadanie 6., strona 122, Matematyka. Klasa 7. Podręcznik – rozwiązania i odpowiedzi

Zadanie 1., strona 81, MATeMAtyka. Klasa 3. Podręcznik. Zakres podstawowy i rozszerzony – rozwiązania i odpowiedzi

Ćwiczenie 3., strona 142, Matematyka. Klasa 2. Podręcznik. Zakres podstawowy - rozwiązania i odpowiedzi

Zadanie 9, strona 103, Matematyka. Klasa 6. Zeszyt ćwiczeń – rozwiązania i odpowiedzi

Zadanie 15., strona 21, Matematyka. Klasa 8. Zbiór zadań - rozwiązania i odpowiedzi

Ćwiczenie 3., strona 8, Matematyka z plusem. Klasa 8. Zeszyt ćwiczeń – rozwiązania i odpowiedzi

Zadanie 5., strona 117, Matematyka. Klasa 7. Zbiór zadań – rozwiązania i odpowiedzi

Zadanie 2.21., strona 327, Prosto do matury. Matematyka. Klasa 2. Podręcznik. Zakres podstawowy i rozszerzony – rozwiązania i odpowiedzi

Zadanie 1.1

5

5

5

5

5

5

5

Zadanie 1.2

5

5

5

5

5

5

5

Zadanie 1.3

5

5

5

5

5

5

5

Zadanie 1.4

5

5

5

5

5

5

5

Zadanie 1.5

6

6

6

6

6

Zadanie 1.6

6

6

6

6

6

6

Zadanie 1.8

6

6

6

Zadanie 1.9

6

6

6

6

6

Zadanie 1.10

6

6

6

Zadanie 1.11

7

7

7

7

7

7

7

Zadanie 1.12

7

7

7

Zadanie 1.13

7

7

7

7

7

Zadanie 1.14

7

7

7

7

7

Zadanie 1.15

8

8

8

8

8

Zadanie 1.16

8

8

8

Zadanie 1.17

8

8

8

8

8

8

Zadanie 1.21

9

9

9

9

9

Zadanie 1.22

9

9

9

9

9

Zadanie 1.23

9

9

9

9

9

Zadanie 1.24

9

9

9

9

9

9

9

Zadanie 1.25

9

9

9

9

Zadanie 1.26

10

10

10

10

10

Zadanie 1.27

10

10

10

10

10

Zadanie 1.28

10

10

10

10

Zadanie 1.29

10

10

10

10

Zadanie 1.30

10

10

10

10

10

Zadanie 1.31

10

10

10

10

10

Zadanie 1.32

11

11

11

11

11

Zadanie 1.33

11

11

11

11

Zadanie 1.34

11

11

11

11

Zadanie 1.35

12

12

12

12

Zadanie 1.36

12

12

12

Zadanie 1.37

12

12

12

12

Zadanie 1.38

12

12

12

12

Zadanie 1.39

12

12

12

12

12

12

12

Zadanie 1.40

13

13

13

13

Zadanie 1.41

13

13

13

13

13

13

13

Zadanie 1.42

13

13

13

13

Zadanie 1.43

13

13

13

Zadanie 1.44

13

13

13

13

Zadanie 1.45

13

13

13

13

13

13

13

Zadanie 1.46

14

14

14

14

14

14

14

Zadanie 1.47

14

14

14

14

14

14

14

Zadanie 1.48

14

14

14

14

14

14

14

Zadanie 1.49

14

14

14

14

14

14

14

Zadanie 1.50

14

14

14

14

14

14

14

Zadanie 1.51

15

15

15

15

15

Zadanie 1.52

15

15

15

15

15

Zadanie 1.53

15

15

15

15

15

15

15

Zadanie 1.54

15

15

15

Zadanie 1.55

15

15

15

15

15

15

15

Zadanie 1.56

15

15

15

Zadanie 1.57

15

15

15

Zadanie 1.58

16

16

16

16

Zadanie 1.59

16

16

16

16

Zadanie 1.60

16

16

16

16

16

16

16

Zadanie 1.61

16

16

16

16

16

Zadanie 1.62

16

16

16

16

16

16

16

Zadanie 1.63

17

17

17

17

17

17

17

Zadanie 1.64

17

17

17

17

17

Zadanie 1.65

17

17

17

17

17

Zadanie 1.66

17

17

17

17

17

17

17

Zadanie 1.67

17

17

17

17

17

17

17

Zadanie 1.68

18

18

18

18

Zadanie 1.70

18

18

18

18

18

18

18

18

18

19

19

19

19

Zadanie 11

19

19

19

19

19

19

19

19

20

20

20

20

Zadanie 19

20

20

20

20

20

Zadanie 20

20

20

20

Zadanie 21

20

20

20

21

21

Zadanie 22

21

21

21

Zadanie 23

21

21

21

21

Zadanie 24

21

21

21

Zadanie 25

21

21

21

21

21

21

21

Zadanie 26

22

22

22

22

22

22

22

Pełny spis treści