Podręcznik, Wydawnictwo: OE Pazdro

Zadanie 1.12, a) - strona 7

Udowodnij, że liczba $\text{[math]}$ jest naturalna.

$\text{[math]}$

$\text{[math]}$

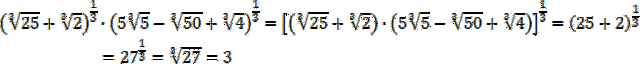
To kończy dowód.

Skorzystaj z tego, że potęgę o wykładniku wymiernym można zapisać za pomocą pierwiastka: $\text{[math]}$ i zauważ wzór skróconego mnożenia na sumę sześcianów: $\text{[math]}$ .

Zadanie 17., strona 16, Matematyka z plusem. Klasa 6. Zeszyt ćwiczeń - rozwiązania i odpowiedzi

Ćwiczenie 1., strona 45, Matematyka z plusem. Klasa 7. Zeszyt ćwiczeń - rozwiązania i odpowiedzi.

Zadanie 7., strona 38, Matematyka z plusem. Klasa 6. Zeszyt ćwiczeń - pytania i odpowiedzi.

Zadanie 2, strona 44, Matematyka. Klasa 5. Zbiór zadań - rozwiązania i odpowiedzi

Zadanie 63., strona 125, Matematyka. Klasa 8. Zbiór zadań - rozwiązania i odpowiedzi

Zadanie 18., strona 162, Matematyka. Klasa 2. Zakres podstawowy. Zbiór zadań - rozwiązania i odpowiedzi

Zadanie 4., strona 207, To się liczy! Klasa 1. Podręcznik – rozwiązania i odpowiedzi

Zadanie 4., strona 139, Matematyka 4. Klasa 4. Zbiór zadań. Zakres rozszerzony - rozwiązania i odpowiedzi

Zadanie 30., strona 292, Prosto do matury. Matematyka. Klasa 1. Zakres podstawowy. Podręcznik - rozwiązania i odpowiedzi

Zadanie 3.34., strona 223, Prosto do matury. Klasa 3. Zakres podstawowy. Podręcznik - rozwiązania i odpowiedzi

Zadanie 1.1

5

5

5

5

5

5

5

Zadanie 1.2

5

5

5

5

5

5

5

Zadanie 1.3

5

5

5

5

5

5

5

Zadanie 1.4

5

5

5

5

5

5

5

Zadanie 1.5

6

6

6

6

6

Zadanie 1.6

6

6

6

6

6

6

Zadanie 1.8

6

6

6

Zadanie 1.9

6

6

6

6

6

Zadanie 1.10

6

6

6

Zadanie 1.11

7

7

7

7

7

7

7

Zadanie 1.12

7

7

7

Zadanie 1.13

7

7

7

7

7

Zadanie 1.14

7

7

7

7

7

Zadanie 1.15

8

8

8

8

8

Zadanie 1.16

8

8

8

Zadanie 1.17

8

8

8

8

8

8

Zadanie 1.21

9

9

9

9

9

Zadanie 1.22

9

9

9

9

9

Zadanie 1.23

9

9

9

9

9

Zadanie 1.24

9

9

9

9

9

9

9

Zadanie 1.25

9

9

9

9

Zadanie 1.26

10

10

10

10

10

Zadanie 1.27

10

10

10

10

10

Zadanie 1.28

10

10

10

10

Zadanie 1.29

10

10

10

10

Zadanie 1.30

10

10

10

10

10

Zadanie 1.31

10

10

10

10

10

Zadanie 1.32

11

11

11

11

11

Zadanie 1.33

11

11

11

11

Zadanie 1.34

11

11

11

11

Zadanie 1.35

12

12

12

12

Zadanie 1.36

12

12

12

Zadanie 1.37

12

12

12

12

Zadanie 1.38

12

12

12

12

Zadanie 1.39

12

12

12

12

12

12

12

Zadanie 1.40

13

13

13

13

Zadanie 1.41

13

13

13

13

13

13

13

Zadanie 1.42

13

13

13

13

Zadanie 1.43

13

13

13

Zadanie 1.44

13

13

13

13

Zadanie 1.45

13

13

13

13

13

13

13

Zadanie 1.46

14

14

14

14

14

14

14

Zadanie 1.47

14

14

14

14

14

14

14

Zadanie 1.48

14

14

14

14

14

14

14

Zadanie 1.49

14

14

14

14

14

14

14

Zadanie 1.50

14

14

14

14

14

14

14

Zadanie 1.51

15

15

15

15

15

Zadanie 1.52

15

15

15

15

15

Zadanie 1.53

15

15

15

15

15

15

15

Zadanie 1.54

15

15

15

Zadanie 1.55

15

15

15

15

15

15

15

Zadanie 1.56

15

15

15

Zadanie 1.57

15

15

15

Zadanie 1.58

16

16

16

16

Zadanie 1.59

16

16

16

16

Zadanie 1.60

16

16

16

16

16

16

16

Zadanie 1.61

16

16

16

16

16

Zadanie 1.62

16

16

16

16

16

16

16

Zadanie 1.63

17

17

17

17

17

17

17

Zadanie 1.64

17

17

17

17

17

Zadanie 1.65

17

17

17

17

17

Zadanie 1.66

17

17

17

17

17

17

17

Zadanie 1.67

17

17

17

17

17

17

17

Zadanie 1.68

18

18

18

18

Zadanie 1.70

18

18

18

18

18

18

18

18

18

19

19

19

19

Zadanie 11

19

19

19

19

19

19

19

19

20

20

20

20

Zadanie 19

20

20

20

20

20

Zadanie 20

20

20

20

Zadanie 21

20

20

20

21

21

Zadanie 22

21

21

21

Zadanie 23

21

21

21

21

Zadanie 24

21

21

21

Zadanie 25

21

21

21

21

21

21

21

Zadanie 26

22

22

22

22

22

22

22

Pełny spis treści