Oblicz pole trójkąta ograniczonego wykresem funkcji
![]() i osiami układu współrzędnych, jeśli do wykresu funkcji liniowej
i osiami układu współrzędnych, jeśli do wykresu funkcji liniowej
![]() należą punkty A(-3,1) oraz B(1,7), a wykres funkcji
należą punkty A(-3,1) oraz B(1,7), a wykres funkcji
![]() jest równoległy do funkcji
jest równoległy do funkcji
![]() i przechodzi przez punkt C(-5,-3).
i przechodzi przez punkt C(-5,-3).
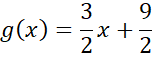
Przecięcie z osią OX:
![]()
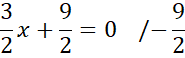
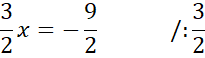
![]()
![]()
Przecięcie z osią OY:
![]()
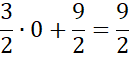
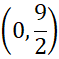
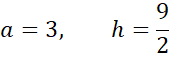
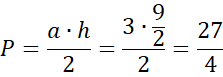

Na podstawie poprzedniego podpunktu znasz wzór funkcji
![]() :
:
![]()
Wyznacz współrzędne przecięcia funkcji z osią OX:
![]() . Aby to zrobić w miejsce
. Aby to zrobić w miejsce
![]() we wzorze funkcji wstaw 0 i z powstałego równania wyznacz wartość
we wzorze funkcji wstaw 0 i z powstałego równania wyznacz wartość
![]()
Wyznacz współrzędne przecięcia funkcji z osią OY:
![]() . Aby to zrobić w miejsce
. Aby to zrobić w miejsce
![]() we wzorze funkcji wstaw 0 i z powstałego równania wyznacz wartość
we wzorze funkcji wstaw 0 i z powstałego równania wyznacz wartość
![]()
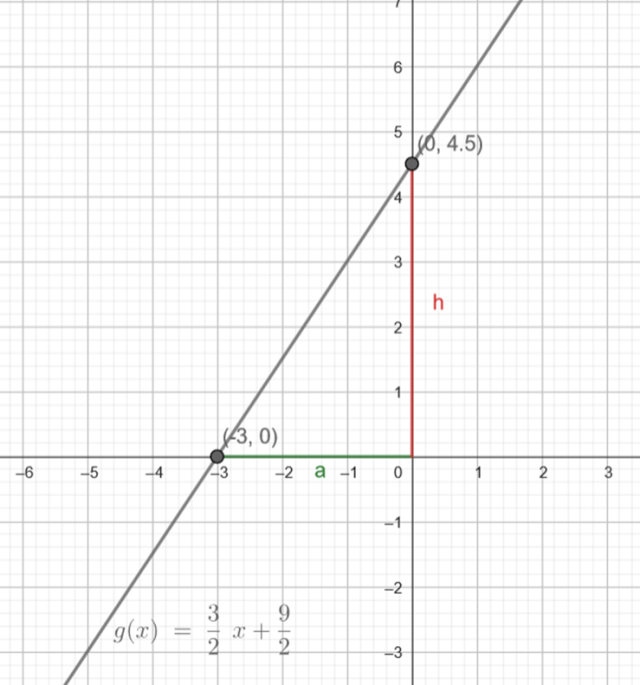
Narysuj w układzie współrzędnych wykres funkcji
![]() i zaznacz na nim wysokość i podstawę, na która opada powstałego trójkąta i oblicz jego pole.
i zaznacz na nim wysokość i podstawę, na która opada powstałego trójkąta i oblicz jego pole.

Zadanie 1
180Zadanie 3
181Zadanie 4
181Zadanie 5
181Zadanie 6
181Zadanie 8
181Zadanie 9
181Zadanie 2
186Zadanie 3
186Zadanie 4
186Zadanie 5
186Zadanie 6
186Zadanie 7
187Zadanie 8
187Zadanie 9
187Zadanie 10
187Zadanie 11
187Zadanie 12
187Zadanie 1
192Zadanie 2
192Zadanie 4
192Zadanie 5
192Zadanie 6
192Zadanie 7
193Zadanie 8
193Zadanie 9
193Zadanie 10
193Zadanie 11
193Zadanie 5
198Zadanie 8
199Zadanie 9
199Zadanie 11
199Zadanie 12
199Zadanie 18
199Zadanie 1
204Zadanie 2
204Zadanie 3
204Zadanie 21
207Zadanie 22
207Zadanie 28
207
