Oblicz dla jakiej wartości
![]() proste
proste
![]() i
i
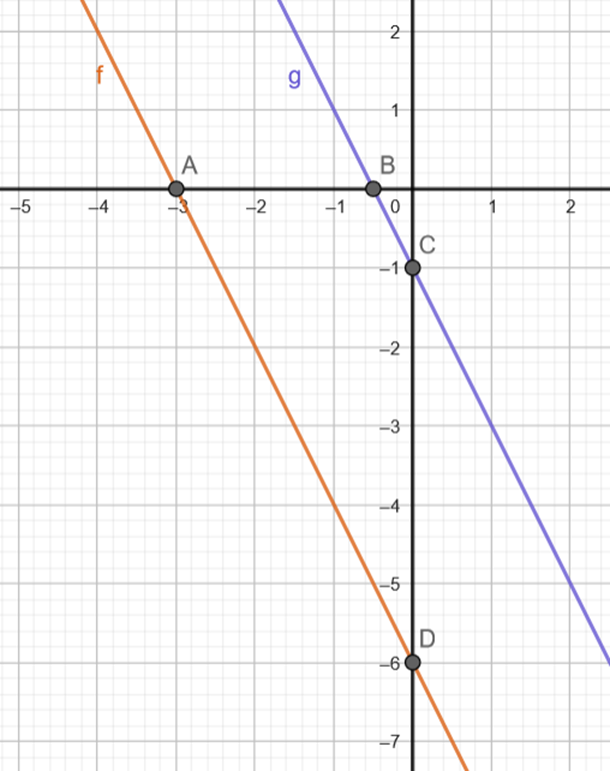
![]() są równoległe oraz zaznacz w układzie współrzędnych trapez, którego podstawy zawierają się w powyższych prostych, a ramiona zawierają się w osiach układu współrzędnych i wyznacz współrzędne jego wierzchołków.
są równoległe oraz zaznacz w układzie współrzędnych trapez, którego podstawy zawierają się w powyższych prostych, a ramiona zawierają się w osiach układu współrzędnych i wyznacz współrzędne jego wierzchołków.
![]()
![]()
![]()
Punkt A: miejsce zerowe funkcji
![]() :
:
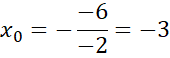
![]()
Punkt B: miejsce zerowe funkcji
![]() :
:
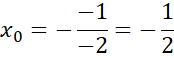
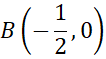
Punkt C: przecięcie wykresu funkcji
![]() z osią OY:
z osią OY:
![]()
Punkt D: przecięcie wykresu funkcji
![]() z osią OY:
z osią OY:
![]()

Z poprzedniego punktu wiesz, że:
![]() .
.
Dla powyższej wartości
![]() wyznacz wzory funkcji
wyznacz wzory funkcji
![]() i
i
![]() Naszkicuj wykresy funkcji w jednym układzie współrzędnych i zaznacz wierzchołki powstałego trapezu.
Naszkicuj wykresy funkcji w jednym układzie współrzędnych i zaznacz wierzchołki powstałego trapezu.
Zauważ, że wierzchołki trapezu są punktami szczególnymi wykresów funkcji
![]() i
i
![]() . Na tej podstawie wyznacz ich współrzędne:
. Na tej podstawie wyznacz ich współrzędne:
Punkt A: miejsce zerowe funkcji
![]() . Punkt B: miejsce zerowe funkcji
. Punkt B: miejsce zerowe funkcji
![]() . Punkt C: przecięcie wykresu funkcji
. Punkt C: przecięcie wykresu funkcji
![]() z osią OY. Punkt D: przecięcie wykresu funkcji
z osią OY. Punkt D: przecięcie wykresu funkcji
![]() z osią OY.
z osią OY.

Zadanie 1
180Zadanie 3
181Zadanie 4
181Zadanie 5
181Zadanie 6
181Zadanie 8
181Zadanie 9
181Zadanie 2
186Zadanie 3
186Zadanie 4
186Zadanie 5
186Zadanie 6
186Zadanie 7
187Zadanie 8
187Zadanie 9
187Zadanie 10
187Zadanie 11
187Zadanie 12
187Zadanie 1
192Zadanie 2
192Zadanie 4
192Zadanie 5
192Zadanie 6
192Zadanie 7
193Zadanie 8
193Zadanie 9
193Zadanie 10
193Zadanie 11
193Zadanie 5
198Zadanie 8
199Zadanie 9
199Zadanie 11
199Zadanie 12
199Zadanie 18
199Zadanie 1
204Zadanie 2
204Zadanie 3
204Zadanie 21
207Zadanie 22
207Zadanie 28
207
