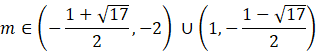
![]()
![]() – największy kąt ostry naprzeciwko najdłuższego boku
– największy kąt ostry naprzeciwko najdłuższego boku
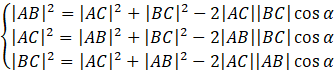
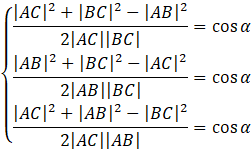
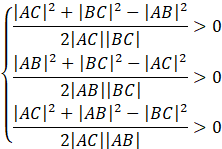
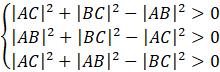
![]()
![]()
![]()
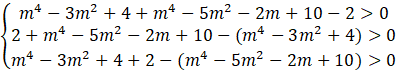
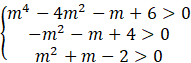
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
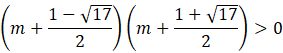
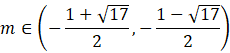
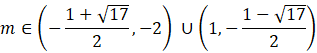
![]()
![]()
![]()
![]()
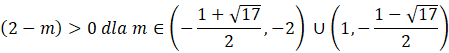
![]()
![]()
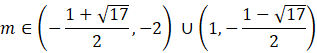
ODP.:
![]()

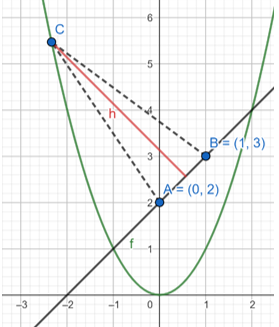
![]()
Skorzystaj z tego, że skoro trójkąt ma być ostry, to cosinus każdego z jego kątów musi być dodatni.
![]() – największy kąt trójkąta ABC
– największy kąt trójkąta ABC
![]()
Twierdzenie cosinusów mówi o tym, że największy kąt znajduję się naprzeciwko najdłuższego boku. Zauważ, że nie wiesz który z boków trójkąta jest najdłuższy. Musisz więc skorzystać z tego twierdzenia dla każdego z boków.
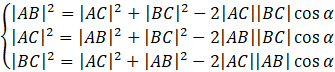
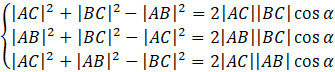
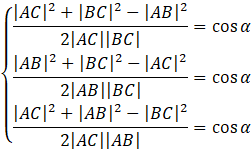
Skorzystaj z tego, że
![]() .
.
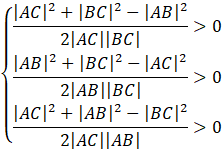
Zauważ, że możesz pomnożyć każdą z nierówności przez jej mianownik. Długość każdego z boków jest dodatnia, więc iloczyn ich i 2 też jest liczbą dodatnią – znak nierówności nie zmieni się.
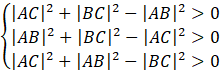
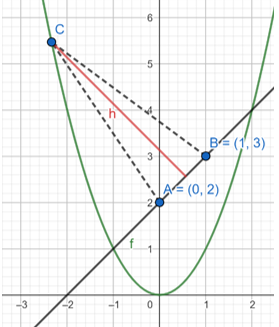
Oblicz długość każdego z boków trójkąta.
![]()
![]()
![]()
Podstaw obliczone długości boków do uzyskanych wcześniej nierówności.
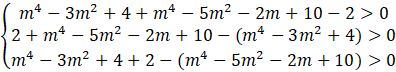
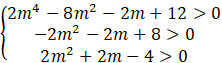
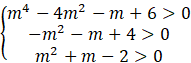
Oblicz dla jakich m spełniona jest każda nierówność.
![]()
Oblicz deltę i miejsca zerowe.
![]()
![]()
![]()
![]()
![]()
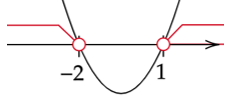
Zapisz do jakiego przedziału należą m dodatnie.
![]()
Oblicz deltę i miejsca zerowe drugiej nierówności.
![]()
![]()
![]()
![]()
![]()
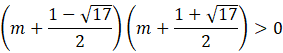
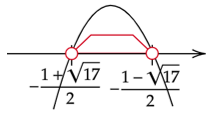
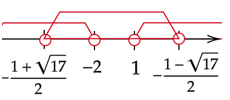
Zapisz do jakiego przedziału należą m dodatnie.
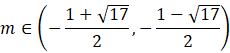
Zapisz iloczyn przedziałów obydwu nierówności.
![]()
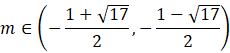
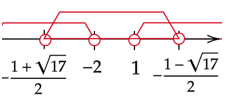
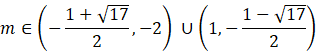
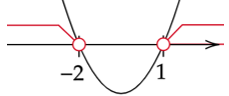
Rozwiąż ostatnią nierówność. Zauważ, że nie da się wyliczyć delty i miejsc zerowych, tak jak w przypadku wcześniejszych przykładów.
![]()
![]()
Rozbij nierówność na dwa nawiasy. Skorzystaj ze wzoru skróconego mnożenia w jednym z nich.
![]()
Kwadrat różnicy jest zawsze większy bądź równy zero
![]() .
.
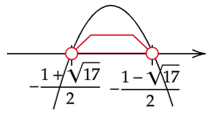
Zauważ, że dla
![]() działanie
działanie
![]() będzie zawsze większe od zera. Ponieważ dla największej wartości do której należą m (
będzie zawsze większe od zera. Ponieważ dla największej wartości do której należą m (
![]() , otrzymasz wynik dodatni.
, otrzymasz wynik dodatni.
![]()
![]()
Ostatnie równanie spełniają
![]() . Więc do tego przedziału należą wartości m ze wszystkich trzech nierówności.
. Więc do tego przedziału należą wartości m ze wszystkich trzech nierówności.