Oblicz promień okręgu O o środku w punkcie
i punkt w którym jest styczny z prostą AB, jeśli 𝐴 = (8, −6) i 𝐵 = (5, 15).
P – punkt przecięcia prostej AB z okręgiem o środku O
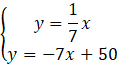
ODP:
Wyznacz równanie prostej AB.
Podstaw współrzędne punktów A i B do wzoru prostej.
Zauważ, że powstał układ równań. Skorzystaj z metody podstawiania.
Przedstaw wzór funkcji liniowej w postaci ogólnej.
Skorzystaj ze wzoru na odległość punktu O=(0,0) od prostej 7x+y-50=0. Będzie to długość promienia r.
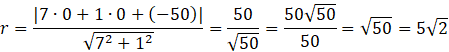
Niech P - punkt przecięcia prostej AB z okręgiem o środku O. Wyznacz równanie prostej OP prostopadłej do prostej AB przechodzącej przez punkt styczności prostej AB i okręgu o środku O.
Współczynnik kierunkowy prostych prostopadłych jest przeciwny i odwrotny.
Prosta OP przechodzi przez punkt O=(0, 0). Podstaw jego współrzędne pod wzór funkcji, aby obliczyć wartość współczynnika b.
Zauważ, że współrzędne punktu P są miejscem przecięcia prostych OP i AB. Powstał układ równań z dwoma niewiadomymi.
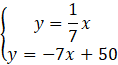
Skorzystaj z metody podstawienia i wyznacz niewiadome.
Zapisz współrzędne punktu P.
