Oblicz dla jakiego m trójmian kwadratowy $\text{[math]}$ ma dwa różne pierwiastki spełniające warunki $\text{[math]}$ .

$\text{[math]}$

ODP: $\text{[math]}$

Równanie ma dwa rozwiązania wtedy gdy delta jest większa od zera. Oblicz dla jakich m: $\text{[math]}$ .

$\text{[math]}$

Zauważ wzór skróconego mnożenia.

$\text{[math]}$

Oblicz dla jakich m wartość po lewej stronie równanie zeruje się.

$\text{[math]}$

Przekształć nierówność $\text{[math]}$ do otrzymania postaci ze wzorami Viete’a.

$\text{[math]}$

Zastosuj wzory Viete’a do powyższego równania.

$\text{[math]}$

Zauważ, że mianownik w otrzymanej nierówności nie może być równy zero.

$\text{[math]}$

Podstaw wyliczone wzory do nierówności

$\text{[math]}$

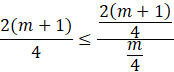
Przenieś wszystkie wartości na lewą stronę i sprowadź ułamki do wspólnego mianownika, aby je odjąć.

$\text{[math]}$

Zauważ, że gdy dzielisz lub mnożysz nierówność przez liczbę ujemną, to jej znak się zmienia. Aby nie było takiej sytuacji pomnóż całą nierówność przez kwadrat mianownika – będziesz mieć pewność, że jest to liczba dodatnia.

$\text{[math]}$

Zauważ, że równanie składa się z iloczynu trzech równań. Będzie ono zerem, jeśli chociaż jeden z nawiasów będzie zerowy. Przyrównaj więc każdy z nich do zera.

$\text{[math]}$

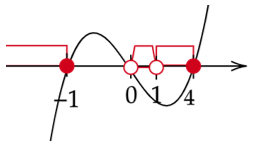
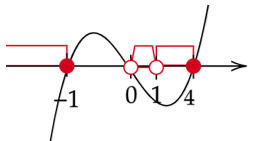
Zaznacz miejsca zerowe na osi, ramiona paraboli skieruj w górę, ponieważ współczynnik przy x z najwyższą potęgą jest dodatni. Zaznacz na niej argumenty, dla których parabola przyjmuje wartości większe bądź równe zero, będzie to rozwiązanie nierówności. Pamiętaj o dziedzinie funkcji, czyli wyklucz obliczone wcześniej wartości m.