Dany jest czworościan foremny o krawędzi 𝑎. Przeprowadzono przez niego płaszczyznę, która zawiera wysokości dwóch ścian bocznych tego czworościanu. Oblicz objętość bryły pozostałej po usunięciu ostrosłupa wyznaczonego przez wyżej wymienioną płaszczyznę.
Naszkicuj sytuację przedstawioną w zadaniu:
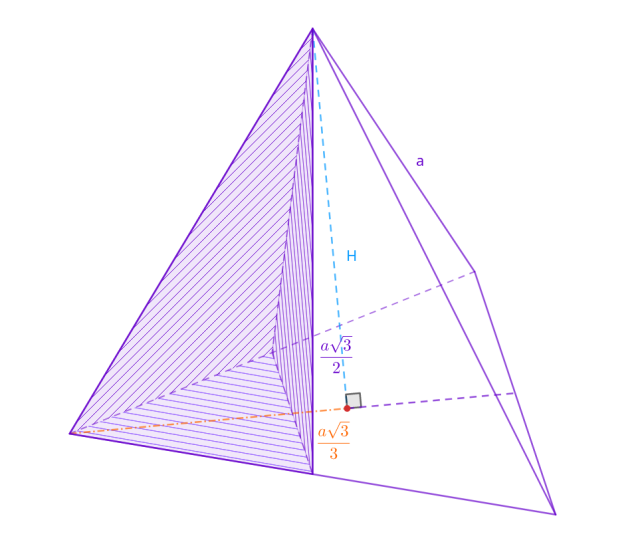
Oblicz wysokość 𝐻 czworościanu foremnego:
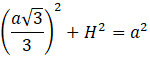
![]()
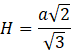
Objętość całego czworościanu foremnego jest więc równa:
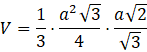
![]()
Objętość zacieniowanego ostrosłupa jest równa:
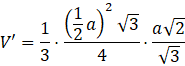
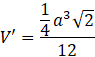
Objętość poszukiwanej bryły jest więc równa:
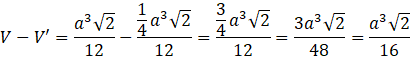
Odp. Objętość bryły pozostałej po odcięciu ostrosłupa jest równa ![]()

Wykorzystaj wzór na wysokość trójkąta równobocznego oraz zależności między długościami w trójkącie równobocznym. Wykorzystaj twierdzenie Pitagorasa, by uzależnić wysokość od długości krawędzi czworościanu. Oblicz objętości dwóch brył, korzystając ze wzoru na objętość ostrosłupa, a następnie ich różnicę.

Ćwiczenie A.
252Ćwiczenie B.
253Ćwiczenie C.
253Zadanie 3.
255Zadanie 7.
256Zadanie 8.
256Zadanie 9.
256Zadanie 10.
257Zadanie 11.
257Zadanie 18.
260Zadanie 19.
260Zadanie 23.
261Zadanie 24.
261Zadanie 25.
261Przykład 1.
263Zadanie 1.
264Zadanie 2.
264Zadanie 5.
264Zadanie 6.
265Zadanie 8.
265Zadanie 9.
265Zadanie 10.
265Ćwiczenie A.
267Przykład 3.
273Zadanie 1.
274Zadanie 4.
274Zadanie 7.
274Zadanie 10.
275Zadanie 11.
275Zadanie 12.
275Zadanie 14.
275Zadanie 17.
276Zadanie 1.
281Zadanie 2.
281Zadanie 3.
281Zadanie 4.
282Zadanie 6.
282Zadanie 8.
282Zadanie 10.
283Zadanie 11.
283Zadanie 12.
283Zadanie 13.
283Zadanie 14.
283Zadanie 19.
284Zadanie S1.
284Ćwiczenie B.
286Zadanie 1.
288Zadanie 2.
288Zadanie 3.
288Zadanie 7.
289Zadanie 9.
289Zadanie 14.
290Zadanie 15.
290Zadanie 3.
292Zadanie 5.
292
