Dany jest przekrój prostopadłościanu przedstawionego na rysunku. Oblicz pole tego przekroju.
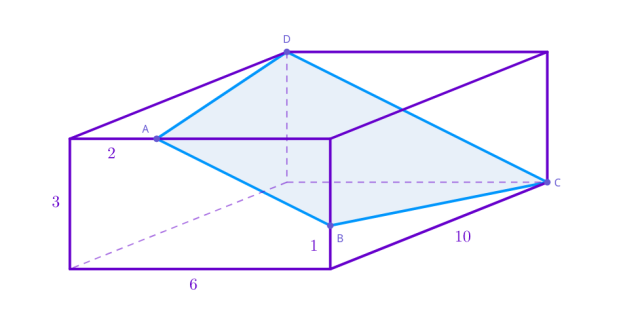
Oblicz długości krawędzi przekroju za pomocą twierdzenia Pitagorasa:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Mamy następujący przekrój:
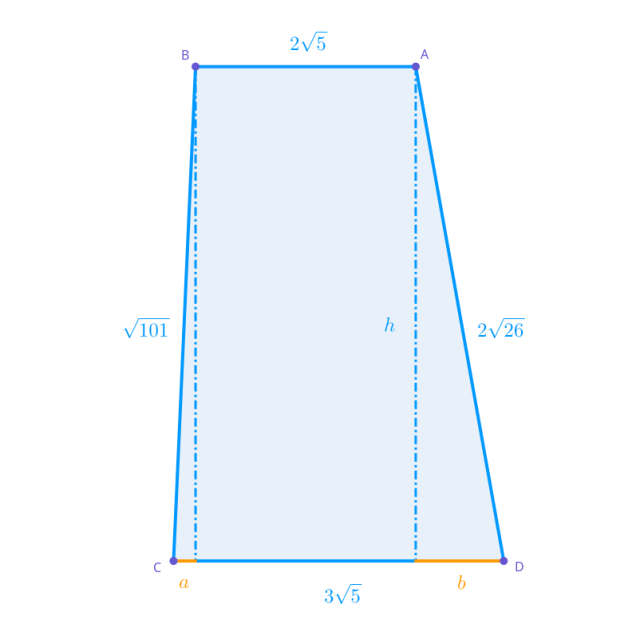
Ułóż i rozwiąż układ równań:
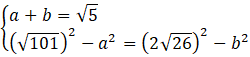
![]()
![]()
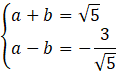
![]()
![]()
![]()
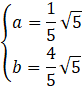
Oblicz wysokość 𝘩 za pomocą twierdzenia Pitagorasa:
![]()
![]()
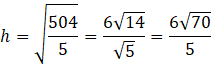
Pole przekroju wynosi zatem:
![]()

Skorzystaj z twierdzenia Pitagorasa, by obliczyć długości boków przekroju. Ułóż układ równań, żeby obliczyć długości odcinków łączących spodki wysokości i wierzchołki ramienia trapezu. Ponownie skorzystaj z twierdzenia Pitagorasa, żeby obliczyć wysokość trapezu. Oblicz pole przekroju.

Ćwiczenie A.
252Ćwiczenie B.
253Ćwiczenie C.
253Zadanie 3.
255Zadanie 7.
256Zadanie 8.
256Zadanie 9.
256Zadanie 10.
257Zadanie 11.
257Zadanie 18.
260Zadanie 19.
260Zadanie 23.
261Zadanie 24.
261Zadanie 25.
261Przykład 1.
263Zadanie 1.
264Zadanie 2.
264Zadanie 5.
264Zadanie 6.
265Zadanie 8.
265Zadanie 9.
265Zadanie 10.
265Ćwiczenie A.
267Przykład 3.
273Zadanie 1.
274Zadanie 4.
274Zadanie 7.
274Zadanie 10.
275Zadanie 11.
275Zadanie 12.
275Zadanie 14.
275Zadanie 17.
276Zadanie 1.
281Zadanie 2.
281Zadanie 3.
281Zadanie 4.
282Zadanie 6.
282Zadanie 8.
282Zadanie 10.
283Zadanie 11.
283Zadanie 12.
283Zadanie 13.
283Zadanie 14.
283Zadanie 19.
284Zadanie S1.
284Ćwiczenie B.
286Zadanie 1.
288Zadanie 2.
288Zadanie 3.
288Zadanie 7.
289Zadanie 9.
289Zadanie 14.
290Zadanie 15.
290Zadanie 3.
292Zadanie 5.
292
