Dany jest sześcian o krawędzi 𝑎oraz jego przekrój przedstawiony na rysunku. Płaszczyzna przekroju jest nachylona pod kątem α do płaszczyzny podstawy. Znajdź miary kąta α, dla których pole przekroju osiąga minimum oraz maksimum. Oblicz te pola.
Wiemy z podpunktu a), że pole przekroju wynosi ![]()
Załóż, że kąt ![]()
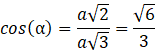
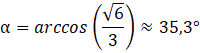
czyli ![]()
Funkcja cosinus maleje na rozpatrywanym przedziale, a im mniejszy mianownik, tym większy ułamek. Oznacza to, że najmniejsze pole przekroju jest dla ![]()
![]()
Minimalne pole:
![]()
Maksymalne pole:
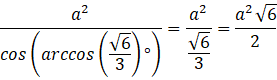

Wykorzystaj wzór na pole wyznaczony w podpunkcie a). Określ dziedzinę, dla której przekrój sześcianu wciąż jest rombem. Zauważ, że cosinus jest monotonicznie malejący na tym przedziale. Oblicz minimum oraz maksimum dla skrajnych wartości wyznaczonego przedziału.

Ćwiczenie A.
252Ćwiczenie B.
253Ćwiczenie C.
253Zadanie 3.
255Zadanie 7.
256Zadanie 8.
256Zadanie 9.
256Zadanie 10.
257Zadanie 11.
257Zadanie 18.
260Zadanie 19.
260Zadanie 23.
261Zadanie 24.
261Zadanie 25.
261Przykład 1.
263Zadanie 1.
264Zadanie 2.
264Zadanie 5.
264Zadanie 6.
265Zadanie 8.
265Zadanie 9.
265Zadanie 10.
265Ćwiczenie A.
267Przykład 3.
273Zadanie 1.
274Zadanie 4.
274Zadanie 7.
274Zadanie 10.
275Zadanie 11.
275Zadanie 12.
275Zadanie 14.
275Zadanie 17.
276Zadanie 1.
281Zadanie 2.
281Zadanie 3.
281Zadanie 4.
282Zadanie 6.
282Zadanie 8.
282Zadanie 10.
283Zadanie 11.
283Zadanie 12.
283Zadanie 13.
283Zadanie 14.
283Zadanie 19.
284Zadanie S1.
284Ćwiczenie B.
286Zadanie 1.
288Zadanie 2.
288Zadanie 3.
288Zadanie 7.
289Zadanie 9.
289Zadanie 14.
290Zadanie 15.
290Zadanie 3.
292Zadanie 5.
292
