Na rysunku obok przedstawiono budowlę w kształcie siatki sześcianu. Wiadomo, że średnica kul zamontowanych na wierzchołkach tego sześcianu jest równa 18 m, natomiast odległość środków tych kul wzdłuż krawędzi sześcianu jest równa 47 m. Prosta wyznaczona przez kule 𝐴 i 𝐻 jest prostopadła do gruntu, natomiast płaszczyzny zawierające kolejno środki kul: 𝐵, 𝐶, 𝐷 i 𝐸, 𝐹, 𝐺 są do gruntu równoległe. Ustal odległości środków wszystkich kul od gruntu.
Zauważ, że środek kuli 𝐴 znajduje się na wysokości promienia kuli nad gruntem, czyli 9 m.
Przekątna 𝐴𝐻 sześcianu ma długość ![]()
![]()
![]()
![]()
Tak jak sugeruje podpowiedź, rozpatrz trójkąt ![]()
![]()
![]()
![]()
Opuść wysokość z wierzchołka 𝐷 na krawędź 𝐴𝐻. Możesz obliczyć jej długość, obliczając wysokość na dwa sposoby:
![]()
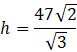
Wykorzystaj fakt, że wysokość opuszczona na przeciwprostokątną w trójkącie prostokątnym dzieli ten trójkąt na trójkąty podobne. Porównaj stosunki odpowiednich długości:
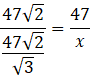
![]()
![]()
Jest to odległość płaszczyzny, na której znajdują się kule ![]()
![]()
![]()
![]()
Zauważ, że trójkąt ![]()
![]()
![]()
Odległość kul 𝐵, 𝐶, 𝐷 od powierzchni ziemi wynosi więc ![]()
Podsumowując:
![]()
![]()
![]()
![]()
![]()

Wykorzystaj długości charakterystycznych odcinków w sześcianie, własności trójkątów prostokątnych oraz podobieństwo figur.

Ćwiczenie A.
252Ćwiczenie B.
253Ćwiczenie C.
253Zadanie 3.
255Zadanie 7.
256Zadanie 8.
256Zadanie 9.
256Zadanie 10.
257Zadanie 11.
257Zadanie 18.
260Zadanie 19.
260Zadanie 23.
261Zadanie 24.
261Zadanie 25.
261Przykład 1.
263Zadanie 1.
264Zadanie 2.
264Zadanie 5.
264Zadanie 6.
265Zadanie 8.
265Zadanie 9.
265Zadanie 10.
265Ćwiczenie A.
267Przykład 3.
273Zadanie 1.
274Zadanie 4.
274Zadanie 7.
274Zadanie 10.
275Zadanie 11.
275Zadanie 12.
275Zadanie 14.
275Zadanie 17.
276Zadanie 1.
281Zadanie 2.
281Zadanie 3.
281Zadanie 4.
282Zadanie 6.
282Zadanie 8.
282Zadanie 10.
283Zadanie 11.
283Zadanie 12.
283Zadanie 13.
283Zadanie 14.
283Zadanie 19.
284Zadanie S1.
284Ćwiczenie B.
286Zadanie 1.
288Zadanie 2.
288Zadanie 3.
288Zadanie 7.
289Zadanie 9.
289Zadanie 14.
290Zadanie 15.
290Zadanie 3.
292Zadanie 5.
292
