Niech dany będzie sześcian o krawędzi długości 1. Płaszczyzna przekroju zawiera krawędź podstawy. Oblicz kąt dwuścienny między płaszczyzną podstawy a płaszczyzną przekroju, dla którego pole przekroju jest o 30% większe od pola ściany sześcianu.
Pole ściany sześcianu wynosi 1² = 1. Oznacza to, że pole przekroju powinno wynosić 1,3. Krawędź przekroju nierównoległa do podstawy ma więc długość ![]()
Wykorzystaj tangens kąta dwuściennego, by sprawdzić, dla jakiego kąta płaszczyzna przekroju przecina przeciwległą ścianę, a dla jakiego podstawę:
![]()
![]()
Czyli dla ![]()
![]()
![]()
![]()
Wykorzystaj definicje funkcji trygonometrycznych, by obliczyć kąt dwuścienny:
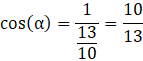
![]()
![]()
![]()
Odp. Kąt dwuścienny powinien wynosić około ![]()
![]()

Sprawdź, czy płaszczyzna przecina przeciwległy bok, czy podstawę. Oblicz wymaganą długość boku, dla którego przekrój ma pole o 30% większe od boku bryły. Wykorzystaj definicje funkcji trygonometrycznych, aby obliczyć kąty dwuścienne, dla których osiągnie oczekiwany wynik.

Ćwiczenie A.
252Ćwiczenie B.
253Ćwiczenie C.
253Zadanie 3.
255Zadanie 7.
256Zadanie 8.
256Zadanie 9.
256Zadanie 10.
257Zadanie 11.
257Zadanie 18.
260Zadanie 19.
260Zadanie 23.
261Zadanie 24.
261Zadanie 25.
261Przykład 1.
263Zadanie 1.
264Zadanie 2.
264Zadanie 5.
264Zadanie 6.
265Zadanie 8.
265Zadanie 9.
265Zadanie 10.
265Ćwiczenie A.
267Przykład 3.
273Zadanie 1.
274Zadanie 4.
274Zadanie 7.
274Zadanie 10.
275Zadanie 11.
275Zadanie 12.
275Zadanie 14.
275Zadanie 17.
276Zadanie 1.
281Zadanie 2.
281Zadanie 3.
281Zadanie 4.
282Zadanie 6.
282Zadanie 8.
282Zadanie 10.
283Zadanie 11.
283Zadanie 12.
283Zadanie 13.
283Zadanie 14.
283Zadanie 19.
284Zadanie S1.
284Ćwiczenie B.
286Zadanie 1.
288Zadanie 2.
288Zadanie 3.
288Zadanie 7.
289Zadanie 9.
289Zadanie 14.
290Zadanie 15.
290Zadanie 3.
292Zadanie 5.
292
