Dany jest pewien ostrosłup o wysokości 𝘩. Przeprowadzono przez niego płaszczyznę równoległą do podstawy w taki sposób, że ostrosłup o podstawie z przekroju ma pole powierzchni całkowitej trzy razy mniejsze od pola powierzchni całej bryły. Wskaż odległość płaszczyzny przekroju od płaszczyzny podstawy.
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Oznacz wysokość ostrosłupa o podstawie z przekroju jako 𝑥. Wiemy, że stosunek pól powierzchni ostrosłupów podobnych wynosi:
![]()
Wylicz skalę podobieństwa tych ostrosłupów:
![]()
![]()
czyli:
![]()
Poszukiwana odległość płaszczyzn to różnica wysokości całego ostrosłupa i wysokości ostrosłupa o podstawie z przekroju, czyli:
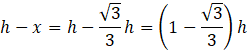
Odp. B. ![]()

Wyznacz skalę podobieństwa figur za pomocą relacji stosunku pól brył podobnych do kwadratu skali. Oblicz wysokość mniejszego, podobnego ostrosłupa i odległość między płaszczyznami: podstawy i przekroju, równą różnicy wysokości całego i mniejszego ostrosłupa.

Ćwiczenie A.
252Ćwiczenie B.
253Ćwiczenie C.
253Zadanie 3.
255Zadanie 7.
256Zadanie 8.
256Zadanie 9.
256Zadanie 10.
257Zadanie 11.
257Zadanie 18.
260Zadanie 19.
260Zadanie 23.
261Zadanie 24.
261Zadanie 25.
261Przykład 1.
263Zadanie 1.
264Zadanie 2.
264Zadanie 5.
264Zadanie 6.
265Zadanie 8.
265Zadanie 9.
265Zadanie 10.
265Ćwiczenie A.
267Przykład 3.
273Zadanie 1.
274Zadanie 4.
274Zadanie 7.
274Zadanie 10.
275Zadanie 11.
275Zadanie 12.
275Zadanie 14.
275Zadanie 17.
276Zadanie 1.
281Zadanie 2.
281Zadanie 3.
281Zadanie 4.
282Zadanie 6.
282Zadanie 8.
282Zadanie 10.
283Zadanie 11.
283Zadanie 12.
283Zadanie 13.
283Zadanie 14.
283Zadanie 19.
284Zadanie S1.
284Ćwiczenie B.
286Zadanie 1.
288Zadanie 2.
288Zadanie 3.
288Zadanie 7.
289Zadanie 9.
289Zadanie 14.
290Zadanie 15.
290Zadanie 3.
292Zadanie 5.
292
