W tym zadaniu musisz wyznaczyć współrzędne wierzchołków trójkąta równobocznego ABC oraz napisać równanie okręgu wpisanego w ten trójkąt.
![]()

Z treści zadania punkt A jest wierzchołkiem paraboli
![]() , stąd
, stąd
![]() . Punkt B leży na jednym z jej ramion, stąd
. Punkt B leży na jednym z jej ramion, stąd
![]() . Punkt C leży do ujemnej półosi OX, stąd
. Punkt C leży do ujemnej półosi OX, stąd
![]() . Zauważ, że:
. Zauważ, że:
![]()
Z tego wynika, że długość boku trójkąta równobocznego ABC wynosi
![]() . Następnie skorzystaj z tego, że dla trójkąta równobocznego wysokość jest równa środkowej, czyli spodek wysokości z wierzchołka B na podstawę AC ma współrzędne:
. Następnie skorzystaj z tego, że dla trójkąta równobocznego wysokość jest równa środkowej, czyli spodek wysokości z wierzchołka B na podstawę AC ma współrzędne:
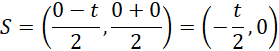
Czyli ten punkt należy do osi OX.
Ze wzoru na wysokość trójkąta równobocznego:
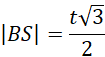
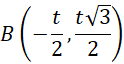
Wynika to z tego, że prosta BS będąca wysokością trójkąta jest prostopadła do osi OX. Współrzędne dla punktu B spełniają warunek:
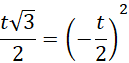
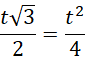
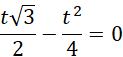
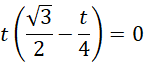
![]()
![]() lub
lub
![]()
Skąd (dla
![]() nie otrzymasz trójkąta):
nie otrzymasz trójkąta):
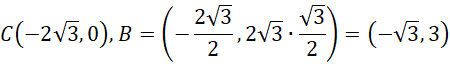
Środek okręgu wpisanego w trójkąt leży na prostej BS (jego pierwsza współrzędna wynosi
![]() ) a promień tego okręgu jest równy jednej trzeciej wysokości, czyli:
) a promień tego okręgu jest równy jednej trzeciej wysokości, czyli:
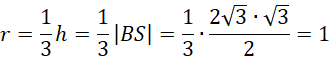
Z tego otrzymasz drugą współrzędną środka okręgu, która wynosi 1. Ostatecznie równanie szukanego okręgu ma postać:
![]()

Ćwiczenie 1.
451Ćwiczenie 2.
453Ćwiczenie 5.
454Zadanie 1.
455Zadanie 8.
455Zadanie 1.
460Zadanie 2.
460Zadanie 3.
460Ćwiczenie 6.
464Zadanie 1.
466Zadanie 2.
466Zadanie 4.
466Zadanie 5.
466Zadanie 1.
471Zadanie 12.
471Zadanie 1.
475Zadanie 2.
475Zadanie 3.
475Zadanie 4.
475Zadanie 5.
475Ćwiczenie 1.
476Ćwiczenie 6.
479Zadanie 1.
482Zadanie 2.
482Zadanie 3.
482Zadanie 7.
482Zadanie 10.
482Zadanie 11.
482Zadanie 13.
495Zadanie 14.
495Zadanie 15.
495Zadanie 16.
495Ćwiczenie 7.
500Ćwiczenie 8.
501Zadanie 4.
503Zadanie 5.
503Zadanie 9.
504Zadanie 10.
504Zadanie 11.
504Zadanie 13.
512Zadanie 14.
512Zadanie 15.
512Zadanie 21.
512Zadanie 22.
512Zadanie 24.
513Zadanie 29.
513Zadanie 30.
513
