W tym zadaniu musisz wyznaczyć punkt na hiperboli przy zadanym warunku.
Szukasz minimum dla funkcji:
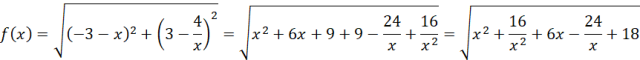
Ponieważ funkcja
![]() jest rosnąca dla
jest rosnąca dla
![]() wystarczy, że znajdziesz minimum funkcji pod pierwiastkiem, to znaczy rozważ pochodną:
wystarczy, że znajdziesz minimum funkcji pod pierwiastkiem, to znaczy rozważ pochodną:
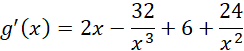
Sprawdzasz, kiedy pochodna się zeruje:
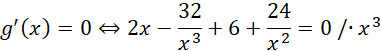
![]()
![]()
![]()
![]()
![]()
![]()
Sprawdź znak drugiej pochodnej dla
![]() (tylko on należy do dziedziny):
(tylko on należy do dziedziny):
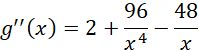
![]()
Druga pochodna w tym punkcie jest dodatnia, dlatego funkcja ma w tym punkcie minimum.
Zatem szukany punkt wynosi:
![]()

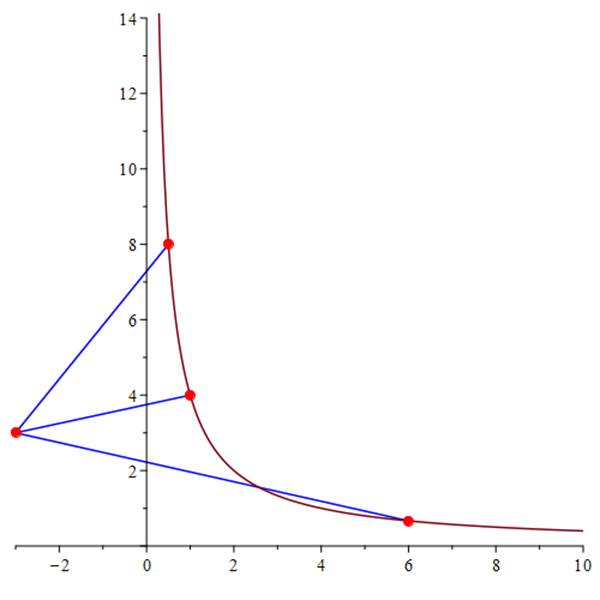
Korzystasz ze wzoru na odległość pomiędzy dwoma punktami:
![]() oraz
oraz
![]() , gdzie:
, gdzie:
![]()
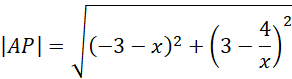

Ćwiczenie 1.
451Ćwiczenie 2.
453Ćwiczenie 5.
454Zadanie 1.
455Zadanie 8.
455Zadanie 1.
460Zadanie 2.
460Zadanie 3.
460Ćwiczenie 6.
464Zadanie 1.
466Zadanie 2.
466Zadanie 4.
466Zadanie 5.
466Zadanie 1.
471Zadanie 12.
471Zadanie 1.
475Zadanie 2.
475Zadanie 3.
475Zadanie 4.
475Zadanie 5.
475Ćwiczenie 1.
476Ćwiczenie 6.
479Zadanie 1.
482Zadanie 2.
482Zadanie 3.
482Zadanie 7.
482Zadanie 10.
482Zadanie 11.
482Zadanie 13.
495Zadanie 14.
495Zadanie 15.
495Zadanie 16.
495Ćwiczenie 7.
500Ćwiczenie 8.
501Zadanie 4.
503Zadanie 5.
503Zadanie 9.
504Zadanie 10.
504Zadanie 11.
504Zadanie 13.
512Zadanie 14.
512Zadanie 15.
512Zadanie 21.
512Zadanie 22.
512Zadanie 24.
513Zadanie 29.
513Zadanie 30.
513
