W tym zadaniu musisz wyznaczyć punkty C i D, dla których czworokąt ABCD jest równoległobokiem o zadanym polu.
![]()
![]()

Zacznij od obliczenia długości odcinka AB oraz równania prostej AB:
![]()
![]()
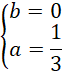
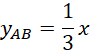
Oblicz wysokość z pola równoległoboku ABCD:
![]()
![]()
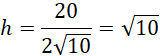
Oznacz
![]() jako spodek wysokości równoległoboku ABCD poprowadzonej z punktu A na podstawę CD. Wtedy:
jako spodek wysokości równoległoboku ABCD poprowadzonej z punktu A na podstawę CD. Wtedy:
![]()
Dodatkowo proste AB i AE są prostopadłe, napisz równanie prostej AE:
![]()
Stąd punkt E ma postać:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Czyli:
![]()
Z uwagi na to, że ABCD jest równoległobokiem proste AB i CD są równoległe, stąd dla:
![]()
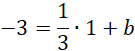
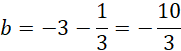
Prosta
![]() ma postać:
ma postać:
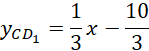
Punkt
![]() obliczysz jako punkt przecięcia tej prostej z prostą:
obliczysz jako punkt przecięcia tej prostej z prostą:
![]()
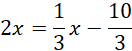
![]()
![]()
![]()
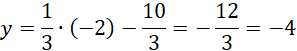
Stąd:
![]()
Wyznacz równanie prostej:
![]()
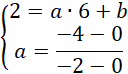
Gdzie drugie równanie wynika z tego, że współczynnik kierunkowy prostej
![]() jest równy współczynnikowi kierunkowemu prostej
jest równy współczynnikowi kierunkowemu prostej
![]() .
.
![]()
![]()
![]()
Wyznacz punkt
![]() , który jest punktem wspólnym prostych
, który jest punktem wspólnym prostych
![]() oraz:
oraz:
![]()
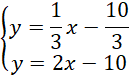
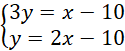
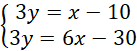
![]()
![]()
![]()
Stąd:
![]()
Analogiczne rozważania tylko dla
![]() doprowadzą cię do tego, że:
doprowadzą cię do tego, że:
![]()

Ćwiczenie 1.
451Ćwiczenie 2.
453Ćwiczenie 5.
454Zadanie 1.
455Zadanie 8.
455Zadanie 1.
460Zadanie 2.
460Zadanie 3.
460Ćwiczenie 6.
464Zadanie 1.
466Zadanie 2.
466Zadanie 4.
466Zadanie 5.
466Zadanie 1.
471Zadanie 12.
471Zadanie 1.
475Zadanie 2.
475Zadanie 3.
475Zadanie 4.
475Zadanie 5.
475Ćwiczenie 1.
476Ćwiczenie 6.
479Zadanie 1.
482Zadanie 2.
482Zadanie 3.
482Zadanie 7.
482Zadanie 10.
482Zadanie 11.
482Zadanie 13.
495Zadanie 14.
495Zadanie 15.
495Zadanie 16.
495Ćwiczenie 7.
500Ćwiczenie 8.
501Zadanie 4.
503Zadanie 5.
503Zadanie 9.
504Zadanie 10.
504Zadanie 11.
504Zadanie 13.
512Zadanie 14.
512Zadanie 15.
512Zadanie 21.
512Zadanie 22.
512Zadanie 24.
513Zadanie 29.
513Zadanie 30.
513
