W tym zadaniu musisz wykazać, że czworokąt ABCD jest prostokątem oraz wyznaczyć równanie okręgu przechodzącego przez wszystkie wierzchołki tego prostokąta.
Aby wykazać to, że czworokąt ABCD jest prostokątem, musisz pokazać, że
![]() oraz
oraz
![]() i
i
![]() oraz
oraz
![]() .
.
Oblicz współczynniki kierunkowe prostych AB, CD, BC oraz AD:
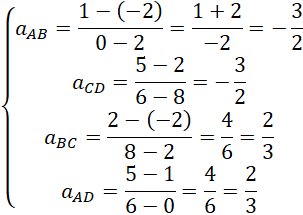
Ponieważ współczynniki AB i CD oraz BC i AD są równe, proste AB i CD oraz BC i AD są równoległe. Ponadto zauważ, że współczynniki kierunkowe prostych AD i DC oraz AB i BC spełniają zależność:
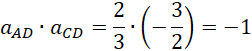
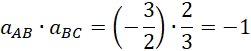
Czyli
![]() oraz
oraz
![]() i
i
![]() oraz
oraz
![]() . To dowodzi, że podany czworokąt ABCD jest prostokątem.
. To dowodzi, że podany czworokąt ABCD jest prostokątem.
Równanie okręgu przechodzącego przez wszystkie wierzchołki tego prostokąta:
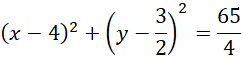

Okrąg przechodzący przez każdy wierzchołek prostokąta ma środek w punkcie przecięcia się przekątnych kwadratu, a jego promień wynosi połowę przekątnej tego prostokąta, stąd:
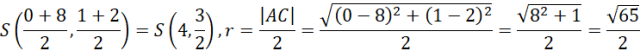
Stąd:
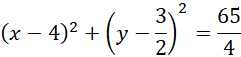

Ćwiczenie 1.
451Ćwiczenie 2.
453Ćwiczenie 5.
454Zadanie 1.
455Zadanie 8.
455Zadanie 1.
460Zadanie 2.
460Zadanie 3.
460Ćwiczenie 6.
464Zadanie 1.
466Zadanie 2.
466Zadanie 4.
466Zadanie 5.
466Zadanie 1.
471Zadanie 12.
471Zadanie 1.
475Zadanie 2.
475Zadanie 3.
475Zadanie 4.
475Zadanie 5.
475Ćwiczenie 1.
476Ćwiczenie 6.
479Zadanie 1.
482Zadanie 2.
482Zadanie 3.
482Zadanie 7.
482Zadanie 10.
482Zadanie 11.
482Zadanie 13.
495Zadanie 14.
495Zadanie 15.
495Zadanie 16.
495Ćwiczenie 7.
500Ćwiczenie 8.
501Zadanie 4.
503Zadanie 5.
503Zadanie 9.
504Zadanie 10.
504Zadanie 11.
504Zadanie 13.
512Zadanie 14.
512Zadanie 15.
512Zadanie 21.
512Zadanie 22.
512Zadanie 24.
513Zadanie 29.
513Zadanie 30.
513
