W tym zadaniu musisz wyznaczyć parametr, dla którego okręgi są styczne wewnętrznie oraz wyznaczyć wspólne stycznych tych okręgów.
![]()

Z postaci okręgów odczytasz, że:
![]()
![]()
Okręgi są styczne wewnętrznie, jeśli:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Dla:
![]()
![]()
![]()
Stąd:
![]()
![]()
![]()
![]()
![]()
![]()
Punkt przecięcia i zarazem punkt styczności tych okręgów wynosi
![]() .
.
Prosta będzie mieć postać:
![]()
![]()
![]()
![]()
![]()
Następnie liczysz odległość środka okręgu
![]() od prostej stycznej, która będzie równa promieniowi:
od prostej stycznej, która będzie równa promieniowi:
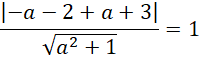
![]()
![]()
Dla:
![]()
![]()
![]()
Stąd:
![]()
![]()
![]()
![]()
![]()
![]()
Punkt przecięcia i zarazem punkt styczności tych okręgów wynosi
![]() .
.
Prosta będzie mieć postać:
![]()

Ćwiczenie 1.
451Ćwiczenie 2.
453Ćwiczenie 5.
454Zadanie 1.
455Zadanie 8.
455Zadanie 1.
460Zadanie 2.
460Zadanie 3.
460Ćwiczenie 6.
464Zadanie 1.
466Zadanie 2.
466Zadanie 4.
466Zadanie 5.
466Zadanie 1.
471Zadanie 12.
471Zadanie 1.
475Zadanie 2.
475Zadanie 3.
475Zadanie 4.
475Zadanie 5.
475Ćwiczenie 1.
476Ćwiczenie 6.
479Zadanie 1.
482Zadanie 2.
482Zadanie 3.
482Zadanie 7.
482Zadanie 10.
482Zadanie 11.
482Zadanie 13.
495Zadanie 14.
495Zadanie 15.
495Zadanie 16.
495Ćwiczenie 7.
500Ćwiczenie 8.
501Zadanie 4.
503Zadanie 5.
503Zadanie 9.
504Zadanie 10.
504Zadanie 11.
504Zadanie 13.
512Zadanie 14.
512Zadanie 15.
512Zadanie 21.
512Zadanie 22.
512Zadanie 24.
513Zadanie 29.
513Zadanie 30.
513
