W tym zadaniu musisz wyznaczyć współrzędne wektora.
![]()

Aby rozwiązać to zadanie, przyjmij, że punkt
![]() spełnia zadane warunki. Jego odległość od zadanej prostej to:
spełnia zadane warunki. Jego odległość od zadanej prostej to:
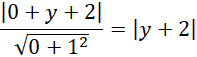
Skorzystałeś tutaj ze wzoru na odległość punktu od prostej. Dodatkowo zauważ, że możesz opuścić wartość bezwzględną, ponieważ punkt nie może leżeć poniżej prostej
![]() . Gdyby tak było, to najkrótszy odcinek łączący punkt
. Gdyby tak było, to najkrótszy odcinek łączący punkt
![]() z okręgiem przecinałby tę prostą a stąd odległość od prostej, byłaby mniejsza niż odległość od okręgu.
z okręgiem przecinałby tę prostą a stąd odległość od prostej, byłaby mniejsza niż odległość od okręgu.
Odległość punktu
![]() od okręgu
od okręgu
![]() , to długość odcinka
, to długość odcinka
![]() pomniejszona o promień okręgu, czyli:
pomniejszona o promień okręgu, czyli:
![]()
Zatem:
![]()
![]()
![]()
Ostatecznie zbiór ten będzie parabolą o równaniu:
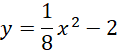
Rysunek poglądowy:
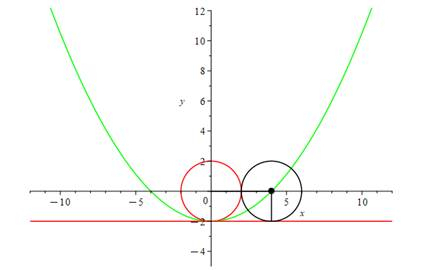
Z rysunki widzisz, że dla
![]() okrąg redukuje się do punktu, dlatego wyrzucasz ten punkt ze zbioru rozwiązań.
okrąg redukuje się do punktu, dlatego wyrzucasz ten punkt ze zbioru rozwiązań.

Ćwiczenie 1.
451Ćwiczenie 2.
453Ćwiczenie 5.
454Zadanie 1.
455Zadanie 8.
455Zadanie 1.
460Zadanie 2.
460Zadanie 3.
460Ćwiczenie 6.
464Zadanie 1.
466Zadanie 2.
466Zadanie 4.
466Zadanie 5.
466Zadanie 1.
471Zadanie 12.
471Zadanie 1.
475Zadanie 2.
475Zadanie 3.
475Zadanie 4.
475Zadanie 5.
475Ćwiczenie 1.
476Ćwiczenie 6.
479Zadanie 1.
482Zadanie 2.
482Zadanie 3.
482Zadanie 7.
482Zadanie 10.
482Zadanie 11.
482Zadanie 13.
495Zadanie 14.
495Zadanie 15.
495Zadanie 16.
495Ćwiczenie 7.
500Ćwiczenie 8.
501Zadanie 4.
503Zadanie 5.
503Zadanie 9.
504Zadanie 10.
504Zadanie 11.
504Zadanie 13.
512Zadanie 14.
512Zadanie 15.
512Zadanie 21.
512Zadanie 22.
512Zadanie 24.
513Zadanie 29.
513Zadanie 30.
513
