W tym zadaniu musisz wyznaczyć na okręgu punktu tak, aby otrzymać trójkąt równoboczny.
![]()

Zacznij od zapisania równania okręgu w postaci kanonicznej:
![]()
![]()
![]()
Stąd:
![]()
Zauważ, że punkt A należy do podanego okręgu:
![]()
Napisz równanie prostej AS:
![]()
![]()
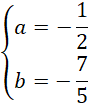
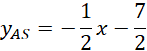
Skorzystaj z zależności między promieniem okręgu opisanego na trójkącie równobocznym a jego wysokością:
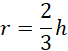
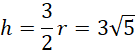
Oznacz E jako spodek wysokości trójkąta równobocznego ABC opuszczonej z wierzchołka A, wtedy:
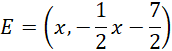
![]()
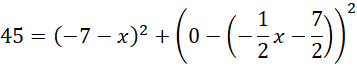
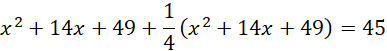
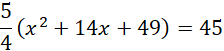
![]()
![]()
![]()
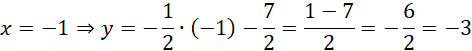
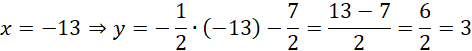
Zauważ, że dla
![]() otrzymasz, a to
otrzymasz, a to
![]() oznacza, że spodek wysokości jest wyżej niż środek okręgu, doprowadzając cię do sprzeczności. Dlatego punkt D ma postać:
oznacza, że spodek wysokości jest wyżej niż środek okręgu, doprowadzając cię do sprzeczności. Dlatego punkt D ma postać:
![]()
Napisz równanie prostej BC, która jest prostopadła do prostej AS oraz przechodzi przez punkt D:
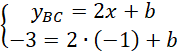
![]()
Oblicz współrzędne punktów B oraz C z przecięcia prostej BC z zadanym okręgiem:

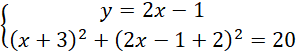
![]()
![]()
![]()
![]()
![]()
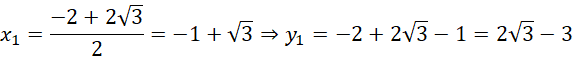
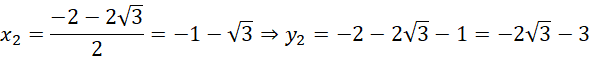
Stąd:
![]()
![]()

Ćwiczenie 1.
451Ćwiczenie 2.
453Ćwiczenie 5.
454Zadanie 1.
455Zadanie 8.
455Zadanie 1.
460Zadanie 2.
460Zadanie 3.
460Ćwiczenie 6.
464Zadanie 1.
466Zadanie 2.
466Zadanie 4.
466Zadanie 5.
466Zadanie 1.
471Zadanie 12.
471Zadanie 1.
475Zadanie 2.
475Zadanie 3.
475Zadanie 4.
475Zadanie 5.
475Ćwiczenie 1.
476Ćwiczenie 6.
479Zadanie 1.
482Zadanie 2.
482Zadanie 3.
482Zadanie 7.
482Zadanie 10.
482Zadanie 11.
482Zadanie 13.
495Zadanie 14.
495Zadanie 15.
495Zadanie 16.
495Ćwiczenie 7.
500Ćwiczenie 8.
501Zadanie 4.
503Zadanie 5.
503Zadanie 9.
504Zadanie 10.
504Zadanie 11.
504Zadanie 13.
512Zadanie 14.
512Zadanie 15.
512Zadanie 21.
512Zadanie 22.
512Zadanie 24.
513Zadanie 29.
513Zadanie 30.
513
