W tym zadaniu musisz pokazać, że dla podanej wartości długość zadanego odcinka jest najkrótsza.
Szukasz minimum dla funkcji:
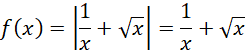
Liczysz pochodną:
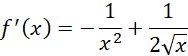
Sprawdzasz, kiedy pochodna się zeruje:
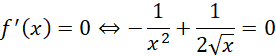
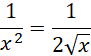
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Sprawdź znak drugiej pochodnej w tym punkcie:
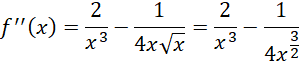
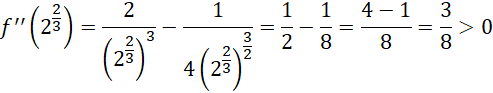
Druga pochodna w tym punkcie jest dodatnia, dlatego funkcja ma w tym punkcie minimum.
Oblicz długość tego odcinka:
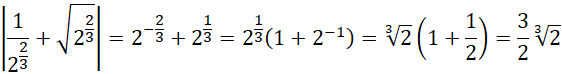
Co należało wykazać.

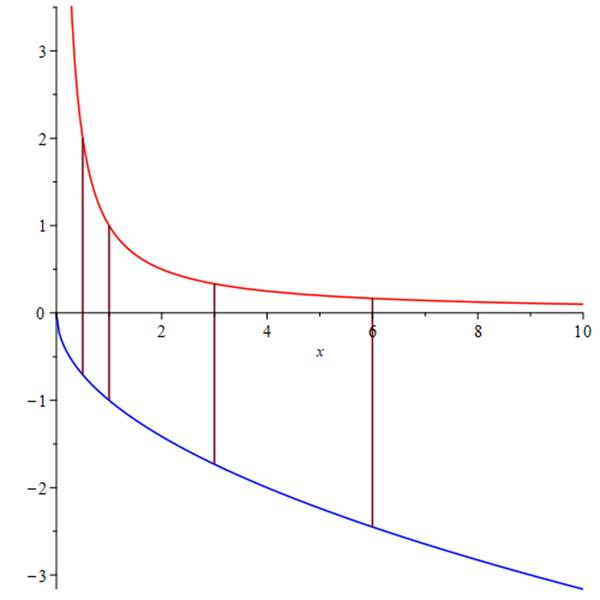
Z wykresu widzisz, że szukane odcinki (kolor bordowy) pomiędzy funkcją
![]() (kolor czerwony) oraz funkcją
(kolor czerwony) oraz funkcją
![]() (kolor niebieski) mają różne długości zależne od argumentu. Długość takiego odcinka zadana jest przez moduł różnicy rzędnych funkcji czerwonej z niebieską, tzn.:
(kolor niebieski) mają różne długości zależne od argumentu. Długość takiego odcinka zadana jest przez moduł różnicy rzędnych funkcji czerwonej z niebieską, tzn.:
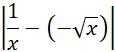
Ponieważ w zadaniu masz znaleźć najmniejszy taki odcinek, definiujesz ten moduł z różnicy jako pewną funkcję, dla której szukasz minimum.

Ćwiczenie 1.
451Ćwiczenie 2.
453Ćwiczenie 5.
454Zadanie 1.
455Zadanie 8.
455Zadanie 1.
460Zadanie 2.
460Zadanie 3.
460Ćwiczenie 6.
464Zadanie 1.
466Zadanie 2.
466Zadanie 4.
466Zadanie 5.
466Zadanie 1.
471Zadanie 12.
471Zadanie 1.
475Zadanie 2.
475Zadanie 3.
475Zadanie 4.
475Zadanie 5.
475Ćwiczenie 1.
476Ćwiczenie 6.
479Zadanie 1.
482Zadanie 2.
482Zadanie 3.
482Zadanie 7.
482Zadanie 10.
482Zadanie 11.
482Zadanie 13.
495Zadanie 14.
495Zadanie 15.
495Zadanie 16.
495Ćwiczenie 7.
500Ćwiczenie 8.
501Zadanie 4.
503Zadanie 5.
503Zadanie 9.
504Zadanie 10.
504Zadanie 11.
504Zadanie 13.
512Zadanie 14.
512Zadanie 15.
512Zadanie 21.
512Zadanie 22.
512Zadanie 24.
513Zadanie 29.
513Zadanie 30.
513
