Dany jest czworościan foremny o długości krawędzi 𝑎 wraz z przekrojem. Oblicz pole tego przekroju.
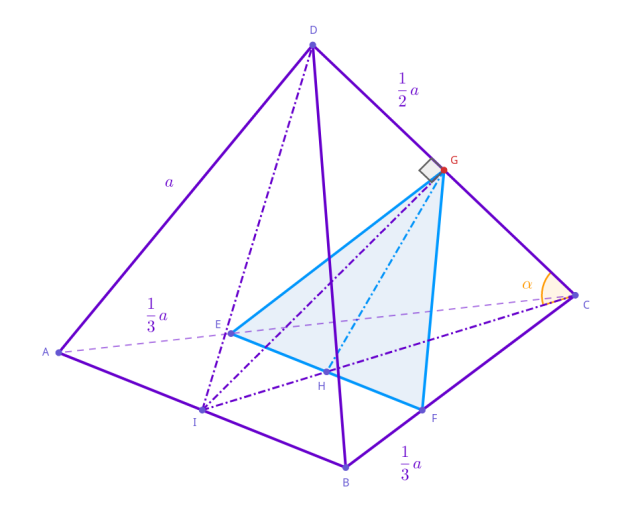
Zauważ, że trójkąty 𝐴𝐵𝐶 i 𝐶𝐸𝐹 są podobne z cechy bkb. Oblicz długość odcinka 𝐸𝐹 za pomocą podobieństwa odpowiednich odcinków:
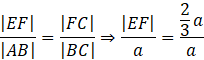
![]()
Trójkąt 𝐶𝐸𝐹 jest równoboczny, więc odcinek 𝐶𝐻 ma długość:
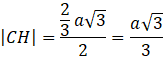
Odcinki: 𝐶𝐼 i 𝐷𝐼 są wysokościami ścian i są równe ![]()
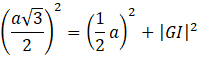
![]()
![]()
Skorzystaj z definicji cosinusa, by obliczyć jego wartość dla kąta α:
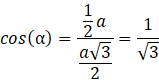
Wykorzystaj twierdzenie cosinusów, żeby obliczyć długość odcinka 𝐺𝐻:
![]()
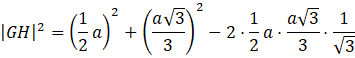
![]()
![]()
Pole przekroju jest równe:
![]()

Skorzystaj z podobieństwa trójkątów w podstawie ostrosłupa, żeby obliczyć długość podstawy przekroju. Wykorzystaj trójkąt utworzony przez krawędź boczną ostrosłupa oraz dwie wysokości ścian bocznych, by wyliczyć cosinus kąta między krawędzią boczną a płaszczyzną podstawy. Oblicz wysokość przekroju za pomocą twierdzenia cosinusów. Oblicz pole przekroju.

Ćwiczenie A.
252Ćwiczenie B.
253Ćwiczenie C.
253Zadanie 3.
255Zadanie 7.
256Zadanie 8.
256Zadanie 9.
256Zadanie 10.
257Zadanie 11.
257Zadanie 18.
260Zadanie 19.
260Zadanie 23.
261Zadanie 24.
261Zadanie 25.
261Przykład 1.
263Zadanie 1.
264Zadanie 2.
264Zadanie 5.
264Zadanie 6.
265Zadanie 8.
265Zadanie 9.
265Zadanie 10.
265Ćwiczenie A.
267Przykład 3.
273Zadanie 1.
274Zadanie 4.
274Zadanie 7.
274Zadanie 10.
275Zadanie 11.
275Zadanie 12.
275Zadanie 14.
275Zadanie 17.
276Zadanie 1.
281Zadanie 2.
281Zadanie 3.
281Zadanie 4.
282Zadanie 6.
282Zadanie 8.
282Zadanie 10.
283Zadanie 11.
283Zadanie 12.
283Zadanie 13.
283Zadanie 14.
283Zadanie 19.
284Zadanie S1.
284Ćwiczenie B.
286Zadanie 1.
288Zadanie 2.
288Zadanie 3.
288Zadanie 7.
289Zadanie 9.
289Zadanie 14.
290Zadanie 15.
290Zadanie 3.
292Zadanie 5.
292
