Dany jest ośmiościan foremny o krawędzi 𝑎, w którym zawarty jest sześcian w taki sposób, że środki ścian bocznych ośmiościanu są jego wierzchołkami. Oblicz długość krawędzi sześcianu i jaką część objętości ośmiościanu foremnego zajmuje ten sześcian.
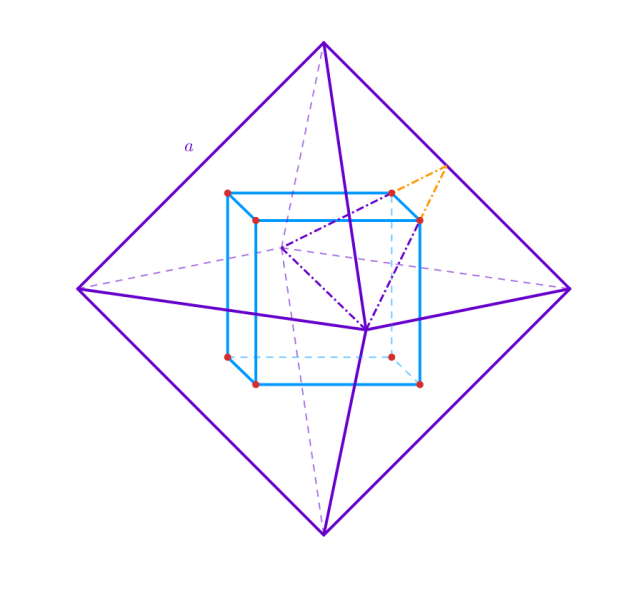
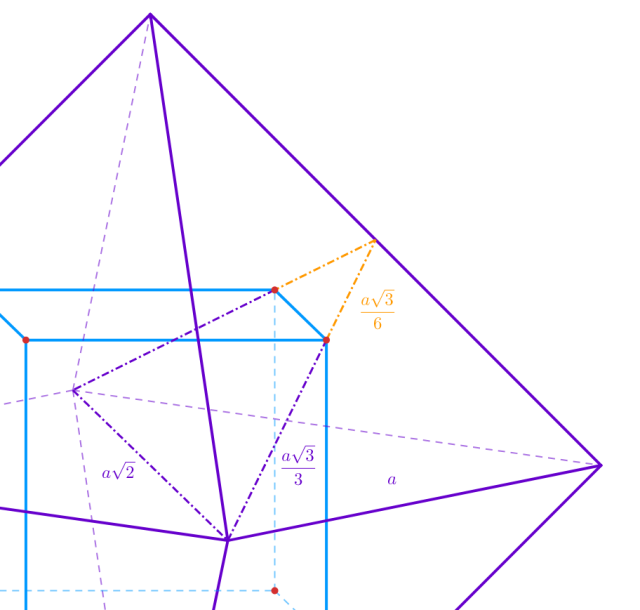
Zauważ, że wierzchołki kwadratu zawierają się w wysokościach ścian ośmiościanu foremnego. Zaznacz trójkąt z dwóch wysokości ścian oraz przekątnej ośmiościanu. Wykorzystaj twierdzenie Talesa oraz fakt, że środek trójkąta równobocznego dzieli jego wysokość w stosunku 1 : 2 i oblicz długość krawędzi wpisanego sześcianu:
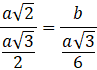
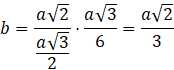
Objętość ośmiościanu to objętość dwóch ostrosłupów o podstawie kwadratu o boku ![]()
![]()
![]()
Objętość wpisanego sześcianu jest równa:
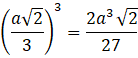
Wpisany sześcian stanowi więc
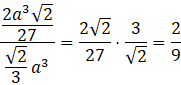
objętości ośmiościanu.

Zauważ, że wierzchołki kwadratu zawierają się w wysokościach ścian ośmiościanu foremnego i wyznacz długości trójkąta rozpiętego na tych wysokościach. Wykorzystaj twierdzenie Talesa lub podobieństwo figur, by wyznaczyć krawędź sześcianu. Wysokość ostrosłupa, z którego składa się ośmiościan, można wyliczyć, wykorzystując twierdzenie Pitagorasa na trójkącie, którego przeciwprostokątną jest krawędź ośmiościanu, a przyprostokątnymi: połowa przekątnej podstawy ostrosłupa i jego wysokość.

Ćwiczenie A.
252Ćwiczenie B.
253Ćwiczenie C.
253Zadanie 3.
255Zadanie 7.
256Zadanie 8.
256Zadanie 9.
256Zadanie 10.
257Zadanie 11.
257Zadanie 18.
260Zadanie 19.
260Zadanie 23.
261Zadanie 24.
261Zadanie 25.
261Przykład 1.
263Zadanie 1.
264Zadanie 2.
264Zadanie 5.
264Zadanie 6.
265Zadanie 8.
265Zadanie 9.
265Zadanie 10.
265Ćwiczenie A.
267Przykład 3.
273Zadanie 1.
274Zadanie 4.
274Zadanie 7.
274Zadanie 10.
275Zadanie 11.
275Zadanie 12.
275Zadanie 14.
275Zadanie 17.
276Zadanie 1.
281Zadanie 2.
281Zadanie 3.
281Zadanie 4.
282Zadanie 6.
282Zadanie 8.
282Zadanie 10.
283Zadanie 11.
283Zadanie 12.
283Zadanie 13.
283Zadanie 14.
283Zadanie 19.
284Zadanie S1.
284Ćwiczenie B.
286Zadanie 1.
288Zadanie 2.
288Zadanie 3.
288Zadanie 7.
289Zadanie 9.
289Zadanie 14.
290Zadanie 15.
290Zadanie 3.
292Zadanie 5.
292
