Dany jest ostrosłup o podstawie trójkąta równoramiennego. Podstawa tego trójkąta ma długość 𝑎. Krawędzie boczne bryły mają długość 𝑏, natomiast kąt dwuścienny między większymi ścianami bocznymi jest równy α. Oblicz pole powierzchni bocznej tego ostrosłupa.
Naszkicuj ostrosłup:
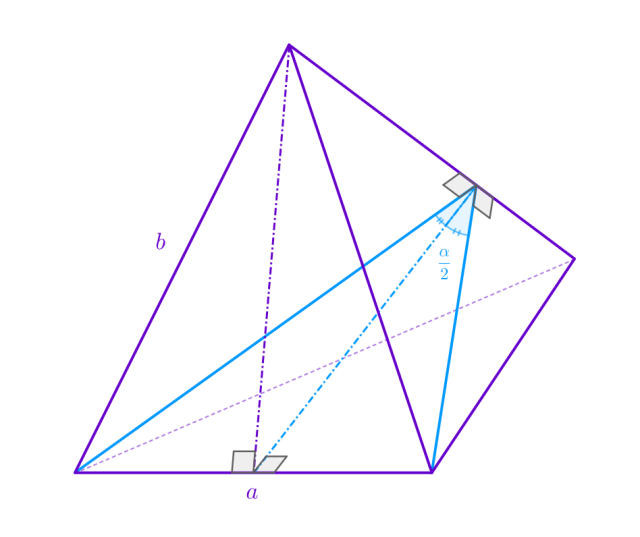
Wyznacz płaszczyznę prostopadłą do dwóch większych ścian bocznych ostrosłupa, zawierającą ich wysokości. Tworzą one niebieski trójkąt równoramienny. Opuść wysokość niebieskiego trójkąta na krawędź podstawy 𝑎. Wyznacza ona dwa trójkąty prostokątne.
Uzależnij długość ramion niebieskiego trójkąta od kąta dwuściennego α oraz długości krawędzi podstawy 𝑎:
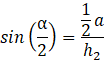
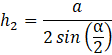
Oblicz pole większej ściany bocznej:
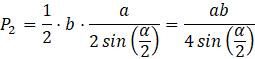
Opuść wysokość krótszej ściany bocznej na podstawę podstawy ostrosłupa. Dzieli ona tę ścianę na dwa przystające trójkąty prostokątne. Oblicz wysokość za pomocą twierdzenia Pitagorasa:
![]()
![]()
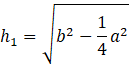
![]()
Oblicz pole mniejszej ściany bocznej:
![]()
Pole powierzchni bocznej ostrosłupa wynosi:
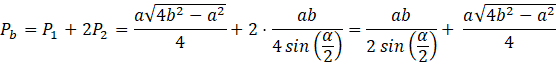
Przekształć wzór na cosinus podwojonego kąta, by wyznaczyć wzór na sinus polowy kąta:
![]()
![]()
![]()
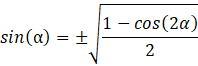
Kąt dwuścienny ![]()
![]()
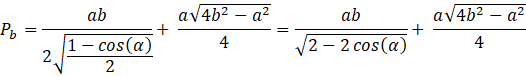
Odp. Wzór na pole boczne ostrosłupa ma postać ![]()

Wyznacz odpowiednią płaszczyznę zawierającą kąt dwuścienny między ścianami. Wykorzystaj zależności w powstałym trójkącie równoramiennym oraz funkcje trygonometryczne, aby uzależnić wysokość ściany bocznej od kąta dwuściennego i długości krawędzi podstawy. Podobnie w mniejszej ścianie bocznej uzależnij wysokość ściany bocznej od krawędzi podstawy oraz krawędzi bocznej za pomocą twierdzenia Pitagorasa. Wykorzystaj wzór na pole powierzchni trójkąta i zsumuj wyniki.

Ćwiczenie A.
252Ćwiczenie B.
253Ćwiczenie C.
253Zadanie 3.
255Zadanie 7.
256Zadanie 8.
256Zadanie 9.
256Zadanie 10.
257Zadanie 11.
257Zadanie 18.
260Zadanie 19.
260Zadanie 23.
261Zadanie 24.
261Zadanie 25.
261Przykład 1.
263Zadanie 1.
264Zadanie 2.
264Zadanie 5.
264Zadanie 6.
265Zadanie 8.
265Zadanie 9.
265Zadanie 10.
265Ćwiczenie A.
267Przykład 3.
273Zadanie 1.
274Zadanie 4.
274Zadanie 7.
274Zadanie 10.
275Zadanie 11.
275Zadanie 12.
275Zadanie 14.
275Zadanie 17.
276Zadanie 1.
281Zadanie 2.
281Zadanie 3.
281Zadanie 4.
282Zadanie 6.
282Zadanie 8.
282Zadanie 10.
283Zadanie 11.
283Zadanie 12.
283Zadanie 13.
283Zadanie 14.
283Zadanie 19.
284Zadanie S1.
284Ćwiczenie B.
286Zadanie 1.
288Zadanie 2.
288Zadanie 3.
288Zadanie 7.
289Zadanie 9.
289Zadanie 14.
290Zadanie 15.
290Zadanie 3.
292Zadanie 5.
292
