Dany jest graniastosłup prawidłowy sześciokątny o krawędzi podstawy 𝑎. Wyznacz wysokości, dla których trójkąt zbudowany z przekątnej ściany bocznej, dłuższej przekątnej podstawy i krótszej przekątnej graniastosłupa jest równoramienny. Rozpatrz wszystkie przypadki.
Naszkicuj sytuację przedstawioną w zadaniu:
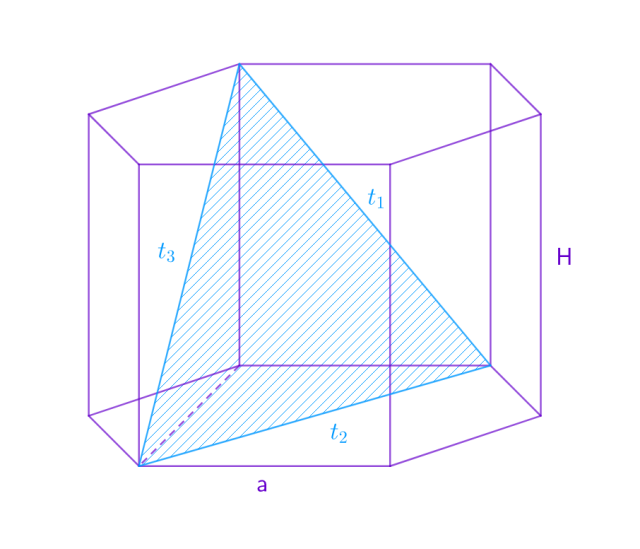
Uzależnij długości: ![]()
![]()
![]()
![]()
![]()
![]()
Przyrównaj kolejne pary boków:
I:
![]()
![]()
![]()
![]()
![]()
II:
![]()
![]()
![]()
![]()
![]()
III:
![]()
![]()
Dwa pierwiastki są sobie równe wtedy i tylko wtedy, gdy wartości pod pierwiastkiem są sobie równe:
![]()
![]()
Otrzymane równanie to sprzeczność, czyli nie istnieje taka wysokość, że boki ![]()
![]()
Odp. Powinien mieć wysokość 𝑎 lub ![]()

Wykorzystaj twierdzenie Pitagorasa, żeby uzależnić krawędzie od krawędzi podstawy oraz wysokości, a następnie rozwiąż odpowiednie równania. Ostatnia równość jest sprzeczna, ponieważ wynika z niej, że bok ma długość zero, co jest niemożliwe w geometrii i stereometrii. Co więcej, równanie to jest niezależne od wysokości.

Ćwiczenie A.
252Ćwiczenie B.
253Ćwiczenie C.
253Zadanie 3.
255Zadanie 7.
256Zadanie 8.
256Zadanie 9.
256Zadanie 10.
257Zadanie 11.
257Zadanie 18.
260Zadanie 19.
260Zadanie 23.
261Zadanie 24.
261Zadanie 25.
261Przykład 1.
263Zadanie 1.
264Zadanie 2.
264Zadanie 5.
264Zadanie 6.
265Zadanie 8.
265Zadanie 9.
265Zadanie 10.
265Ćwiczenie A.
267Przykład 3.
273Zadanie 1.
274Zadanie 4.
274Zadanie 7.
274Zadanie 10.
275Zadanie 11.
275Zadanie 12.
275Zadanie 14.
275Zadanie 17.
276Zadanie 1.
281Zadanie 2.
281Zadanie 3.
281Zadanie 4.
282Zadanie 6.
282Zadanie 8.
282Zadanie 10.
283Zadanie 11.
283Zadanie 12.
283Zadanie 13.
283Zadanie 14.
283Zadanie 19.
284Zadanie S1.
284Ćwiczenie B.
286Zadanie 1.
288Zadanie 2.
288Zadanie 3.
288Zadanie 7.
289Zadanie 9.
289Zadanie 14.
290Zadanie 15.
290Zadanie 3.
292Zadanie 5.
292
