Dany jest stożek o wysokości 𝘩 oraz promieniu podstawy 𝑟. Wpisano w niego sześcian tak, że jedna ze ścian należy do płaszczyzny podstawy, a wierzchołki przeciwległej ściany należą do powierzchni bocznej stożka. Wyznacz wzór na objętość wpisanego sześcianu.
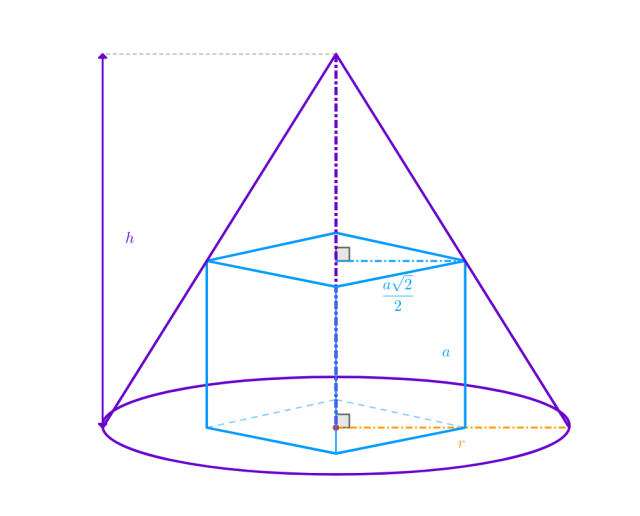
Zauważ, że trójkąt prostokątny utworzony przez połowę przekątnej ściany bocznej sześcianu jest podobny do trójkąta prostokątnego tworzącego stożek opisany. Wykorzystaj tę relację, by uzależnić długość krawędzi sześcianu od wysokości i promienia podstawy:
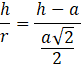
![]()
![]()
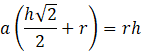
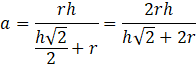
Objętość wpisanego sześcianu wynosi:
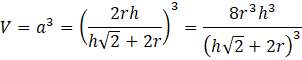

Zauważ trójkąt podobny utworzony przez charakterystyczną krawędź sześcianu wpisanego. Wykorzystaj relacje między odcinkami w figurach podobnych, by wyznaczyć długość krawędzi 𝑎 sześcianu. Podnieś otrzymane wyrażenie do trzeciej potęgi, żeby otrzymać szukane wyrażenie.

Ćwiczenie A.
252Ćwiczenie B.
253Ćwiczenie C.
253Zadanie 3.
255Zadanie 7.
256Zadanie 8.
256Zadanie 9.
256Zadanie 10.
257Zadanie 11.
257Zadanie 18.
260Zadanie 19.
260Zadanie 23.
261Zadanie 24.
261Zadanie 25.
261Przykład 1.
263Zadanie 1.
264Zadanie 2.
264Zadanie 5.
264Zadanie 6.
265Zadanie 8.
265Zadanie 9.
265Zadanie 10.
265Ćwiczenie A.
267Przykład 3.
273Zadanie 1.
274Zadanie 4.
274Zadanie 7.
274Zadanie 10.
275Zadanie 11.
275Zadanie 12.
275Zadanie 14.
275Zadanie 17.
276Zadanie 1.
281Zadanie 2.
281Zadanie 3.
281Zadanie 4.
282Zadanie 6.
282Zadanie 8.
282Zadanie 10.
283Zadanie 11.
283Zadanie 12.
283Zadanie 13.
283Zadanie 14.
283Zadanie 19.
284Zadanie S1.
284Ćwiczenie B.
286Zadanie 1.
288Zadanie 2.
288Zadanie 3.
288Zadanie 7.
289Zadanie 9.
289Zadanie 14.
290Zadanie 15.
290Zadanie 3.
292Zadanie 5.
292
