Dany jest pewien stożek. Kulę o średnicy 6 cm można wpisać w ten stożek. Kulę o średnicy 8 cm styczną do powierzchni bocznej stożka jego podstawa dzieli na dwie półkule. Oblicz wysokość stożka.
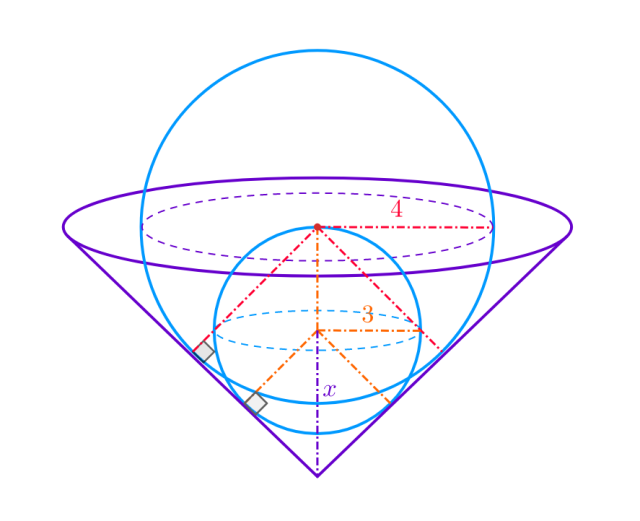
Naszkicuj dane podane w zadaniu na jednym rysunku. Zauważ, że trójkąt utworzony przez wysokość stożka, promień większej kuli oraz wiodącą stożka jest podobny do trójkąta utworzonego przez promień mniejszej kuli. Oznacz przeciwprostokątną mniejszego trójkąta jako 𝑥 i wykorzystaj twierdzenie Talesa:
![]()
![]()
![]()
Odp. Wysokość stożka jest równa 12 cm.

Zauważ, że podana w zadaniu konstrukcja tworzy trójkąty podobne. Wykorzystaj własności figur podobnych, by wyliczyć brakujące długości.

Ćwiczenie A.
252Ćwiczenie B.
253Ćwiczenie C.
253Zadanie 3.
255Zadanie 7.
256Zadanie 8.
256Zadanie 9.
256Zadanie 10.
257Zadanie 11.
257Zadanie 18.
260Zadanie 19.
260Zadanie 23.
261Zadanie 24.
261Zadanie 25.
261Przykład 1.
263Zadanie 1.
264Zadanie 2.
264Zadanie 5.
264Zadanie 6.
265Zadanie 8.
265Zadanie 9.
265Zadanie 10.
265Ćwiczenie A.
267Przykład 3.
273Zadanie 1.
274Zadanie 4.
274Zadanie 7.
274Zadanie 10.
275Zadanie 11.
275Zadanie 12.
275Zadanie 14.
275Zadanie 17.
276Zadanie 1.
281Zadanie 2.
281Zadanie 3.
281Zadanie 4.
282Zadanie 6.
282Zadanie 8.
282Zadanie 10.
283Zadanie 11.
283Zadanie 12.
283Zadanie 13.
283Zadanie 14.
283Zadanie 19.
284Zadanie S1.
284Ćwiczenie B.
286Zadanie 1.
288Zadanie 2.
288Zadanie 3.
288Zadanie 7.
289Zadanie 9.
289Zadanie 14.
290Zadanie 15.
290Zadanie 3.
292Zadanie 5.
292
